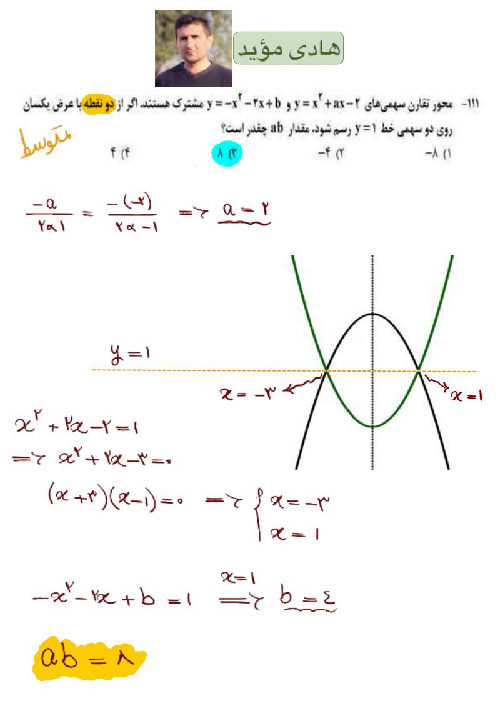
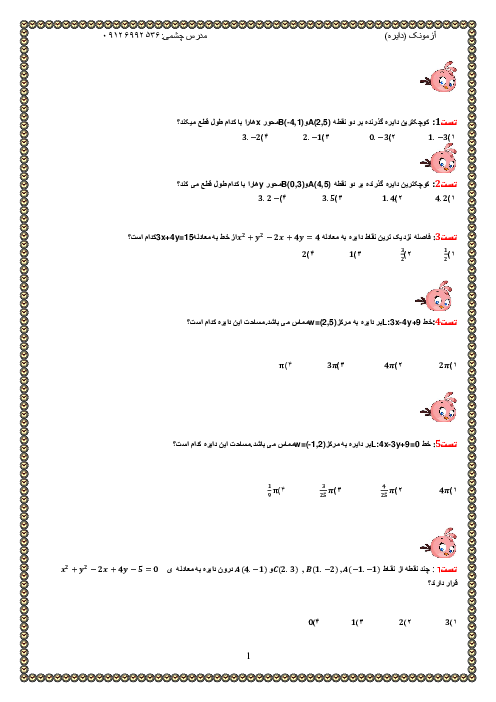
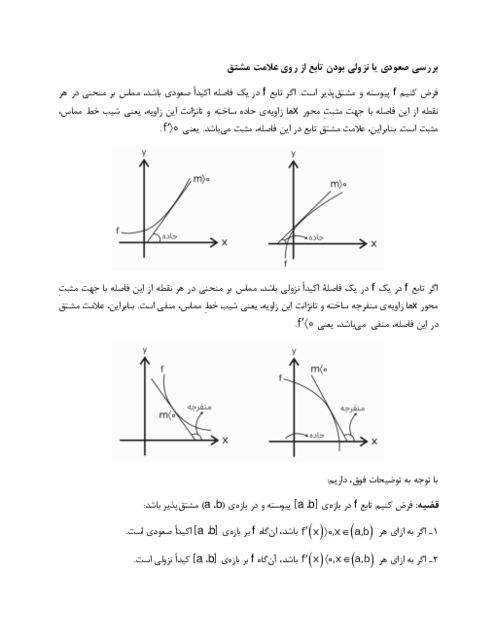
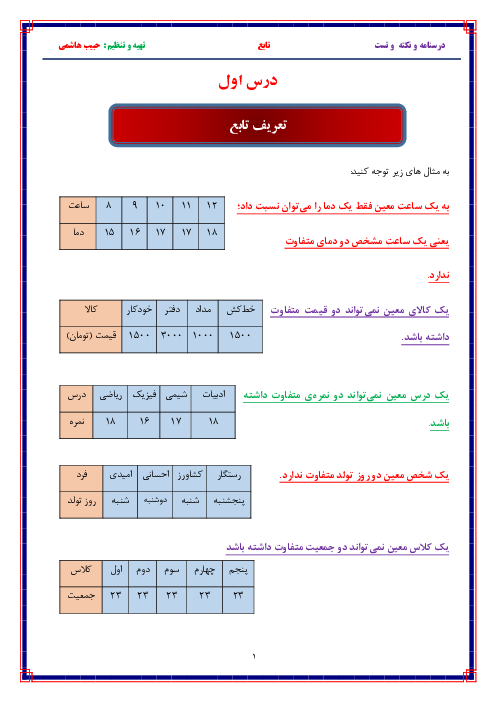
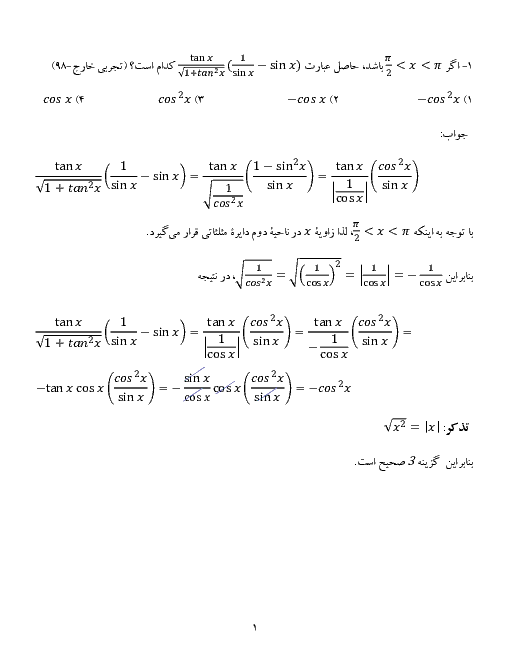
تابع با ضابطهٔ $f(x)=\frac{ax-\sqrt[3]{{{x}^{2}}-1}}{4{{x}^{n}}-12}$ را در نظر بگیرید. اگر $\underset{x\to \infty }{\mathop{\lim }}\,f(x)=\frac{1}{6}$ باشد، آنگاه $\underset{x\to 3}{\mathop{\lim }}\,f(x)$ کدام است؟
$\frac{1}{24}$
2 )
$\frac{1}{18}$
3 )
$\frac{1}{12}$
4 )
$\frac{5}{36}$
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...