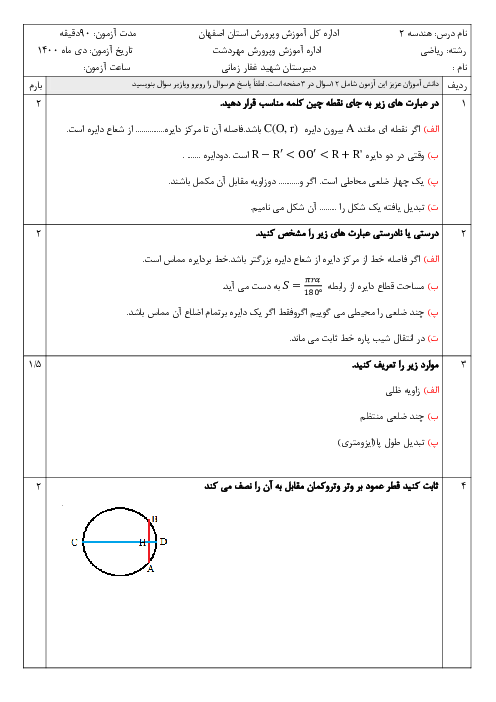
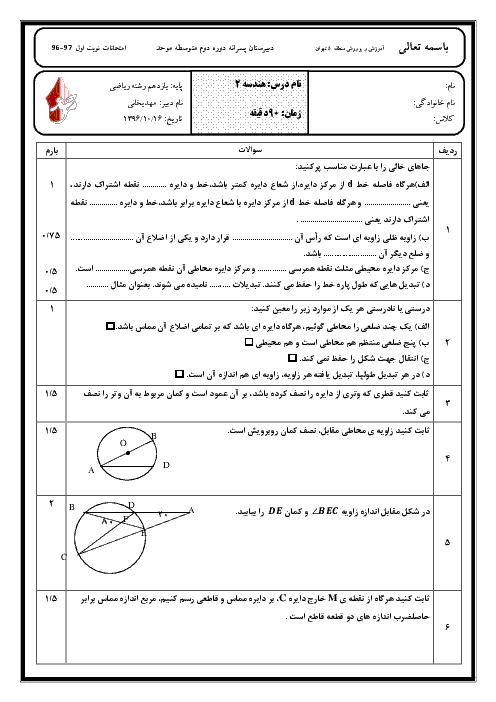
مساحت قطاعی از دایرهٔ با زاویهٔ مرکزی را و مساحت قطاعی از دایرهٔ و با زاویهٔ مرکزی را می‌نامیم. نسبت کدام است؟

گاما رو نصب کن!

درحال دریافت اطلاعات ...

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

نوبت اول گام به گام کاربرگ آزمون عملکردی پودمان آزمون پیشرفت تحصیلی طرح درس نمونه سوال تست پاورپوینت علوم هشتم فارسی چهارم ریاضی هفتم علوم نهم گزارش کارورزی

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

درس 1: مفاهیم اولیه و زاویه‌ها در دایره هندسه (2) یازدهم دوره دوم متوسطه- نظری علوم ریاضی درسنامه آموزشی این مبحث

مساحت قطاعی از دایرهٔ ${{C}_{1}}({{O}_{1}},3)$ با زاویهٔ مرکزی ${{160}^{\circ }}$ را ${{S}_{1}}$ و مساحت قطاعی از دایرهٔ ${{C}_{2}}({{O}_{2}},6)$ و با زاویهٔ مرکزی ${{120}^{\circ }}$ را ${{S}_{2}}$ می‌نامیم. نسبت $\frac{{{S}_{2}}}{{{S}_{1}}}$ کدام است؟

1 )

$\frac{3}{2}$

2 )

$\frac{9}{4}$

3 )

$3$

4 )

$\frac{16}{3}$

نمایش پاسخ

مساحت قطاعی از دایرهٔ‌ $C(O,R)$ که زاویهٔ مرکزی آن $\alpha$ باشد، برابر است با:

$S=\frac{\pi {{R}^{2}}\alpha }{360}$.

$\Rightarrow \frac{{{S}_{2}}}{{{S}_{1}}}={{(\frac{{{R}_{2}}}{{{R}_{1}}})}^{2}}\times \frac{{{\alpha }_{2}}}{{{\alpha }_{1}}}={{(\frac{6}{3})}^{2}}\times \frac{120}{160}=4\times \frac{3}{4}=3$

گزارش اشکال

یک تست دیگه بزن

یک آزمون کامل بده