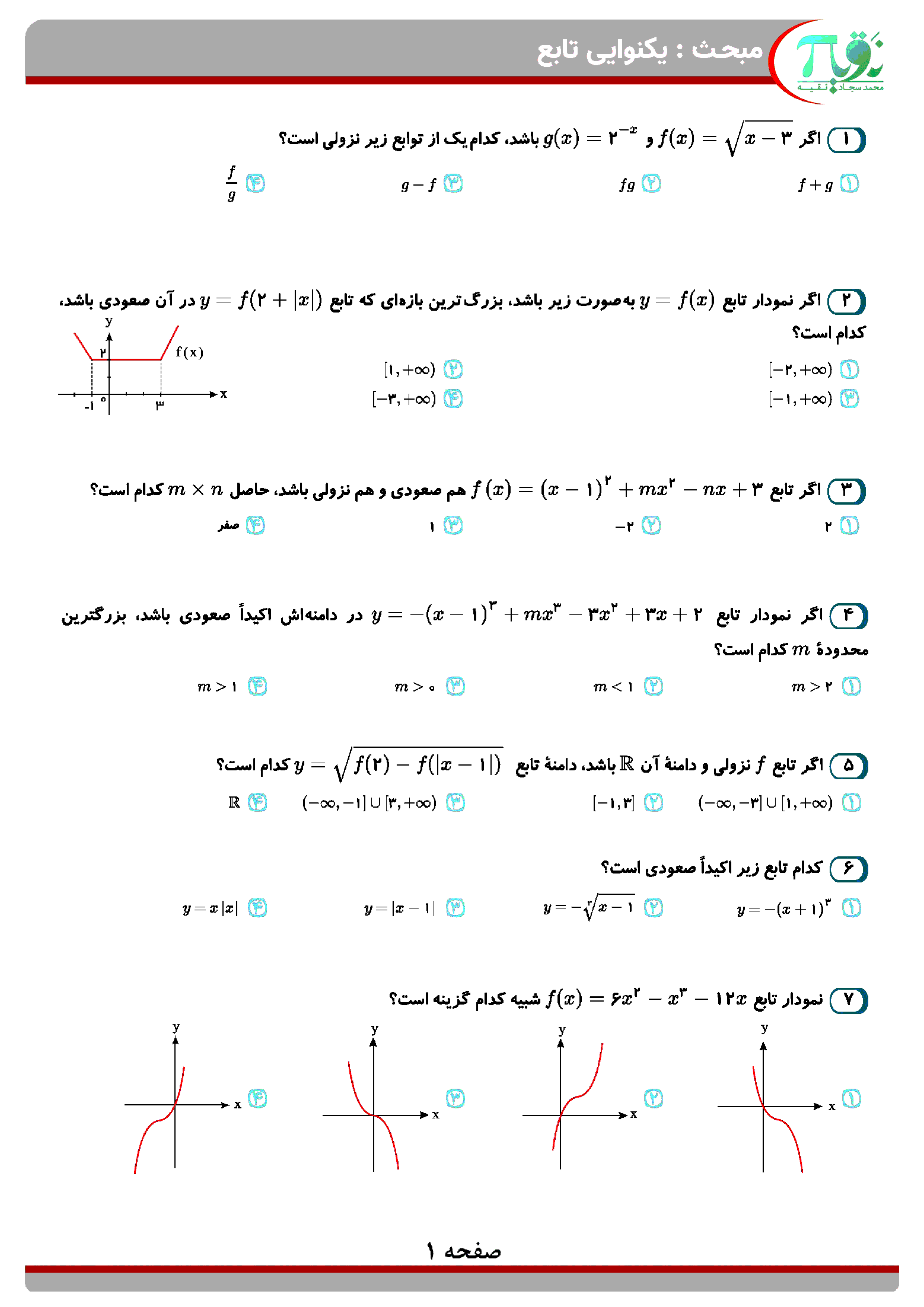
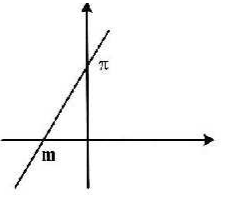
شکل زیر، نمودار تابع ${f^{ - 1}}$ را نشان میدهد. اگر $\mathop {\lim }\limits_{x \to + \infty } \frac{{{f^{ - 1}}(x)}}{{f(x)}} = \pi $ باشد، مقدار m کدام است؟
$ - \sqrt \pi $
2 )
$ - \frac{1}{{\sqrt \pi }}$
3 )
$ - \frac{1}{\pi }$
4 )
$ - \pi \sqrt \pi $
پاسخ تشریحی :
تحلیل ویدئویی تست
محسن ذوالفقاری 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...