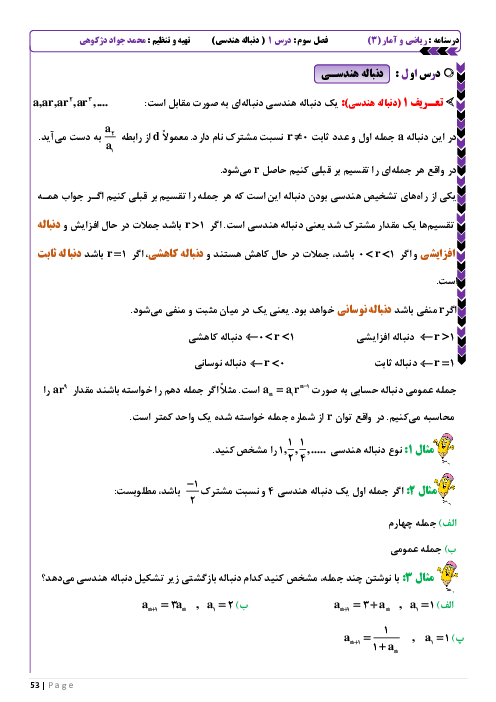
نكته: جملۀ عمومی يك دنبالۀ هندسی با جملۀ اول ${{a}_{1}}$ و نسبت‌مشترك $r$ به‌صورت ${{a}_{n}}={{a}_{1}}{{r}^{n-1}}$ است.

نكته: مجموع جملات يك دنبالۀ هندسی با جملۀ اول ${{a}_{1}}$ و نسبت‌مشترك $r$ برابر است با: ${{S}_{n}}=\frac{{{a}_{1}}\left( 1-{{r}^{n}} \right)}{1-r}$

اعداد $384,192,96,...,3$ تشكيل يك دنبالۀ هندسی می‌دهند كه مجموع آن‌ها خواسته شده است. ابتدا بايد تعداد جملات را به‌دست آوريم، داريم:

$\left\{ \begin{matrix}    {{a}_{1}}=384  \\    r=\frac{192}{384}=\frac{1}{2}  \\ \end{matrix}\Rightarrow {{a}_{n}}=384\times {{\left( \frac{1}{2} \right)}^{n-1}} \right.=\frac{384}{{{2}^{n-1}}}$ 

${{a}_{n}}=3\Rightarrow \frac{384}{{{2}^{n-1}}}=3\Rightarrow {{2}^{n-1}}=\frac{384}{3}=128\Rightarrow {{2}^{n-1}}={{2}^{7}}\Rightarrow n=8$

بنابراین:

${{S}_{8}}=\frac{{{a}_{1}}\left( 1-{{\left( \frac{1}{2} \right)}^{8}} \right)}{1-\frac{1}{2}}=\frac{384\times \left( \frac{255}{256} \right)}{\frac{1}{2}}=384\times \frac{255}{128}=765$