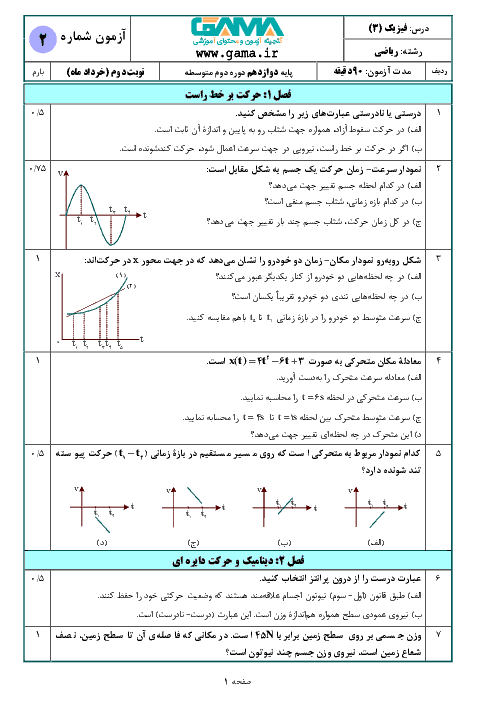
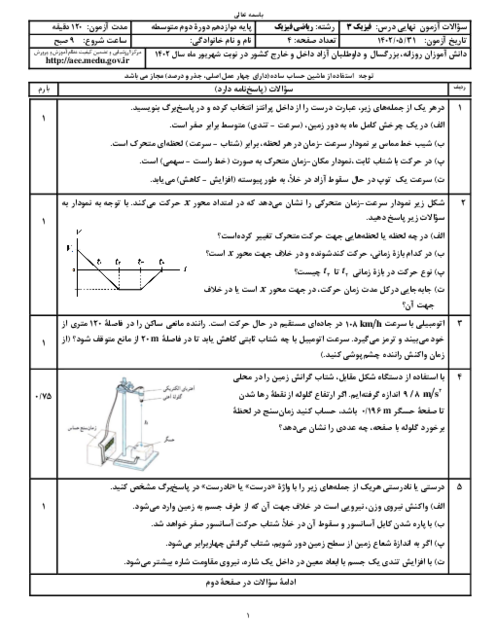
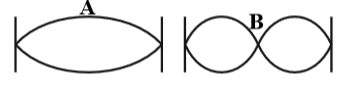ابتدا نسبت تندی موج را در دو ریسمان به‌دست می‌آوریم:

$\mu =\frac{m}{L}\Rightarrow \frac{{{\mu }_{B}}}{{{\mu }_{A}}}=\frac{{{m}_{B}}}{{{m}_{A}}}\times \frac{{{L}_{A}}}{{{L}_{B}}}$

$xrightarrow[{{L}_{A}}={{L}_{B}}]{{{m}_{B}}=2{{m}_{A}}}\Rightarrow \frac{{{\mu }_{B}}}{{{\mu }_{A}}}=2$

$v=\sqrt{\frac{F}{\mu }}\Rightarrow \frac{{{v}_{A}}}{{{v}_{B}}}=\sqrt{\frac{{{F}_{A}}}{{{F}_{B}}}\times \frac{{{\mu }_{B}}}{{{\mu }_{A}}}}\xrightarrow{{{F}_{B}}=\frac{1}{2}{{F}_{A}}}\frac{{{v}_{A}}}{{{v}_{B}}}=\sqrt{4}=2$

حال با استفاده از رابطهٔ بسامدهای تشدیدی تار، داریم:

$f=\frac{nv}{2L}\Rightarrow \frac{{{f}_{A}}}{{{f}_{B}}}=\frac{{{n}_{A}}}{{{n}_{B}}}\times \frac{{{v}_{A}}}{{{v}_{B}}}\times \frac{{{L}_{B}}}{{{L}_{A}}}$

$\xrightarrow[{{v}_{A}}=2{{v}_{B}},{{L}_{A}}={{L}_{B}}]{{{f}_{A}}={{f}_{B}}}1=\frac{{{n}_{A}}}{{{n}_{B}}}\times 2\times 1\Rightarrow \frac{{{n}_{B}}}{{{n}_{A}}}=2$

یعنی تعداد شکم‌ها در ریسمان B دو برابر تعداد شکم‌ها در ریسمان A است. پس گزینه «4» درست است.