درس 1: آشنایی با منطق ریاضی
آمار و احتمال
یازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
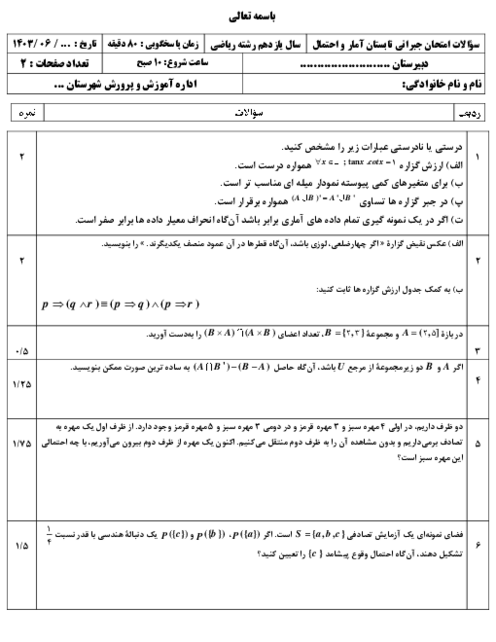
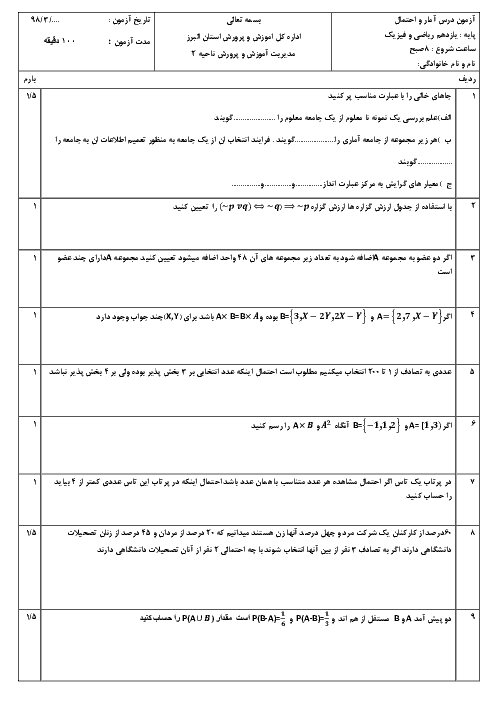
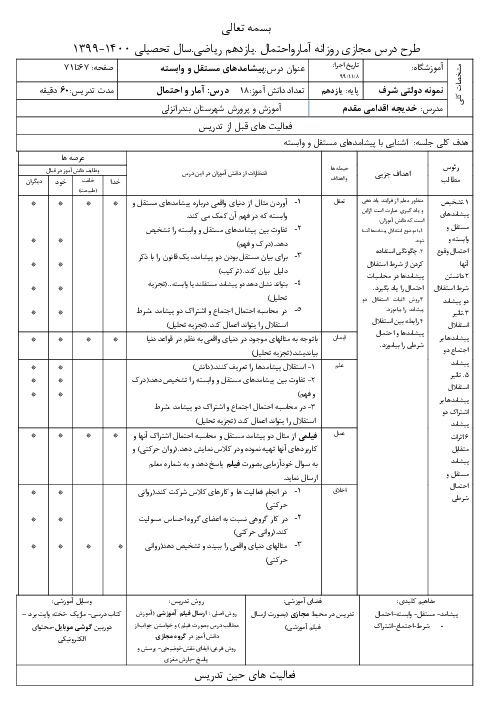
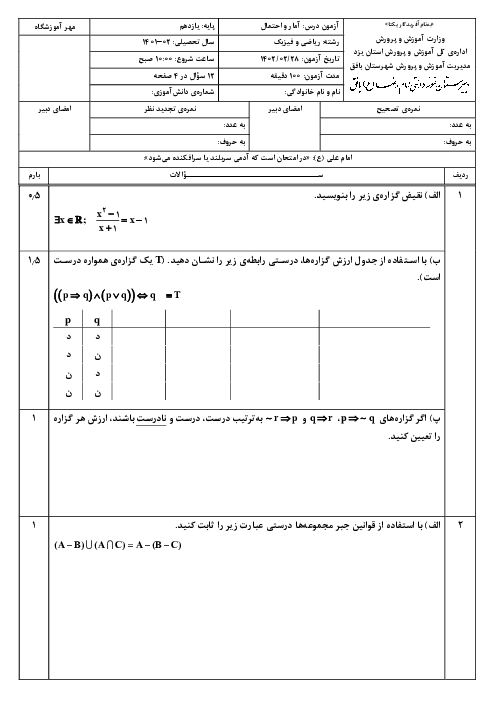
ارزش گزاره‌ی سوری زیر و نقیض آن، به‌ترتیب در کدام گزینه آمده است؟
$\exists x\in \mathbb{N};({{x}^{2}}\le 4\wedge \frac{-2}{x}=1)$
1 )
درست - $\forall x\in \mathbb{N};({{x}^{2}}\gt 4\vee \frac{-2}{x}\ne 1)$
2 )
درست - $\forall x\in \mathbb{N};({{x}^{2}}\gt 4\wedge \frac{-2}{x}\ne 1)$
3 )
نادرست - $\forall x\in \mathbb{N};({{x}^{2}}\gt 4\wedge \frac{-2}{x}\ne 1)$
نادرست - $\exists x\in \mathbb{N};({{x}^{2}}\gt 4\vee \frac{-2}{x}\ne 1)$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...