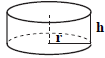
تابع هزينۀ ساخت اين مخزن به صورت زير است.
$C=\pi {{r}^{2}}\times 300+2\pi r\times h\times 400$
همچنين حجم مخزن برابر $6\pi $ متر مكعب است، پس:
$\pi {{r}^{2}}h=6\pi \Rightarrow h=\frac{6}{{{r}^{2}}}$
بنابراين تابع هزينه برحسب شعاع قاعده برابر است با:
$C(r)=300\pi {{r}^{2}}+\frac{4800\pi }{r}$
میخواهيم مينيمم نسبی تابع به دست آمده را محاسبه كنيم:
${C}'(r)=600\pi r-\frac{4800\pi }{{{r}^{2}}}=0\Rightarrow 600\pi r=\frac{4800\pi }{{{r}^{2}}}\Rightarrow {{r}^{3}}=8\Rightarrow r=2$
تنها نقطۀ بحرانی تابع هزينه در $r=2$ اتفاق میافتد. اين نقطه مينيمم نسبی تابع است و داريم:
$h=\frac{6}{{{r}^{2}}}=\frac{6}{{{2}^{2}}}=\frac{6}{4}=1/5$