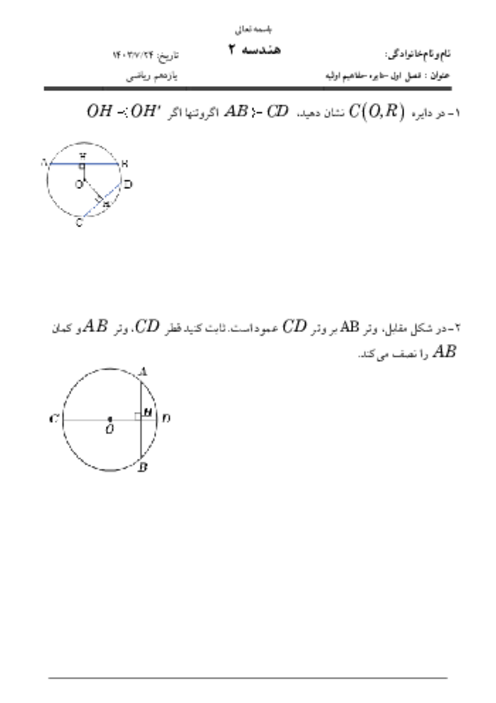
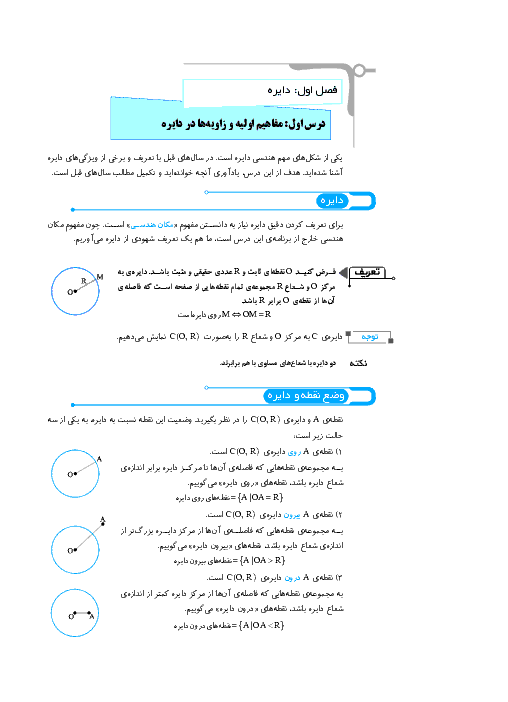
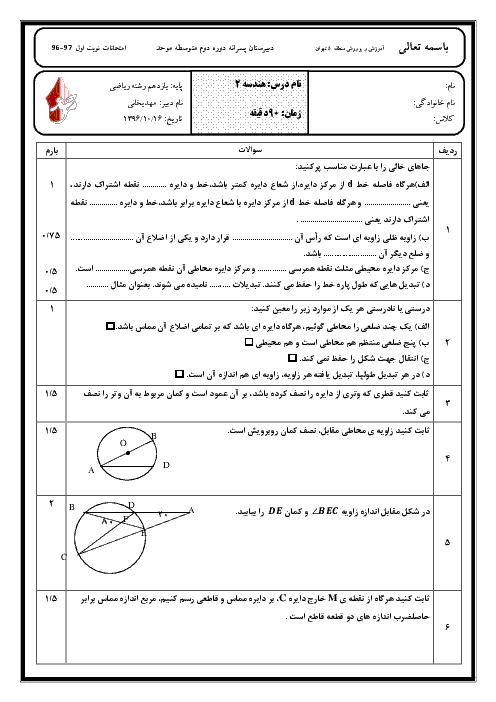
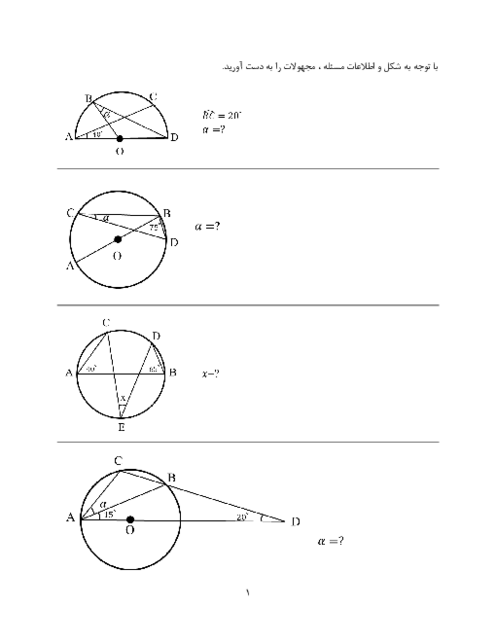
دو خط عمود بر هم $d$ و ${d}'$ مفروض‌اند. نقاط صفحه را ابتدا نسبت به خط $d$ و سپس تصاویر آنها را نسبت به ${d}'$ بازتاب می‌دهیم. اگر ترکیب این دو بازتاب را یک تبدیل فرض کنیم، کدام گزاره در مورد این تبدیل همواره درست است؟
این تبدیل، شیب خطوط و جهت اشکال را حفظ می‌کند.
2 )
این تبدیل، شیب خطوط و جهت اشکال را حفظ نمی‌کند.
3 )
این تبدیل، شیب خطوط را حفظ کرده ولی جهت اشکال را حفظ نمی‌کند.
4 )
این تبدیل، جهت اشکال را حفظ کرده ولی شیب خطوط را حفظ نمی‌کند.
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...