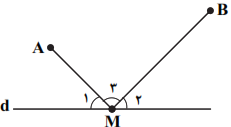
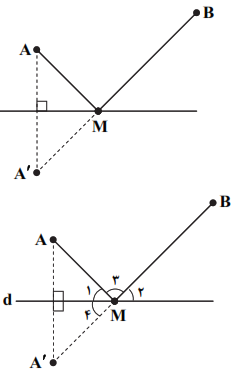
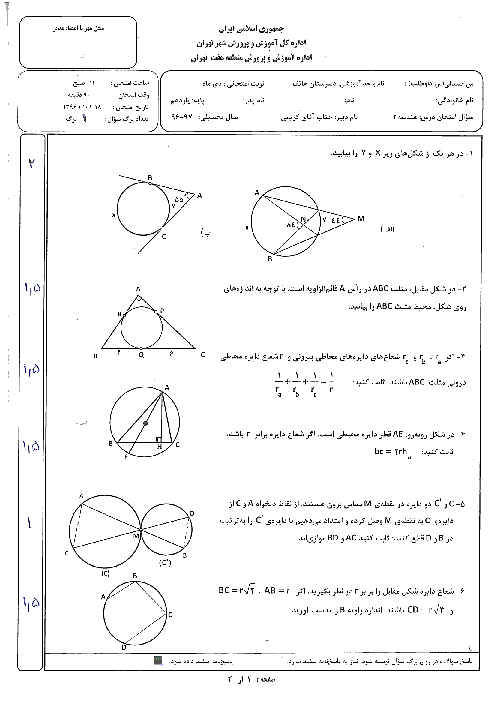
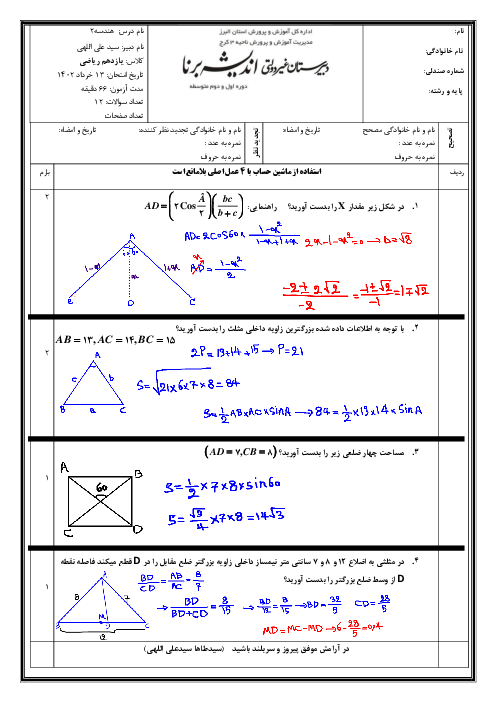
نكته (مسئلهی هرون براي پيدا كردن كوتاهترين مسير): در شكل زیر برای بهدست آوردن محل نقطهی M روی خط d بهطوریکه $AM+MB$ کمترین مقدار ممکن باشد، ابتدا بازتاب A نسبت به خط d را بهدست میآوریم و آنرا ${A}'$ مینامیم. خط فرضی ${A}'B$، خط d را در یک نقطه قطع میکند. این نقطه همان نقطهی M موردنظر است.
نکته: اگر بازتاب نقطهی A نسبت به خط d نقطهی ${A}'$ باشد و $A\ne {A}'$، آ»گاه d عمودمنصف $A{A}'$ است.
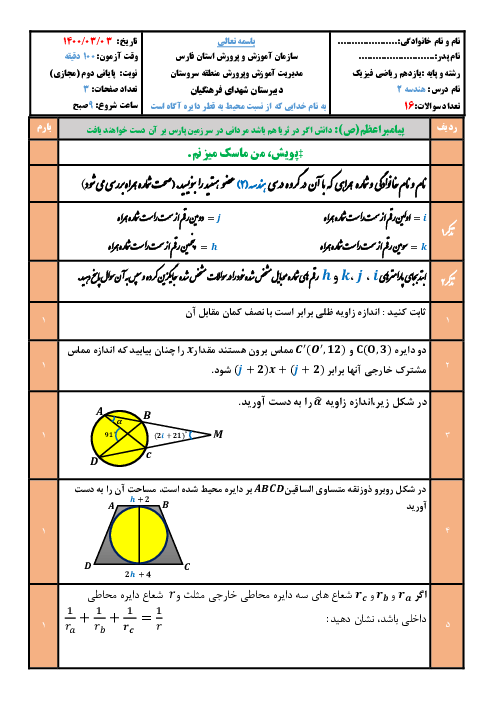
با توجه به نكات بالا، در شكل زیر چون ${A}'$ بازتاب A نسبت به d است داریم:
$(*)\,\,\,\,{{\hat{M}}_{1}}={{\hat{M}}_{4}}$
از طرفی ${{\hat{M}}_{2}}$ و ${{\hat{M}}_{4}}$ متقابل به رأس هستند، پس:
$(**)\,\,\,\,{{\hat{M}}_{2}}={{\hat{M}}_{4}}$
از $(*)$ و $(**)$ داریم:
${{\hat{M}}_{1}}={{\hat{M}}_{2}}$
بنابراین گزینهی 4 پاسخ است.