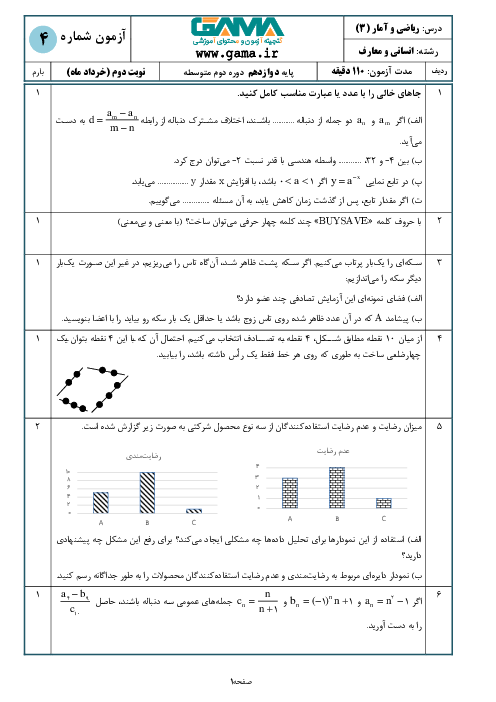
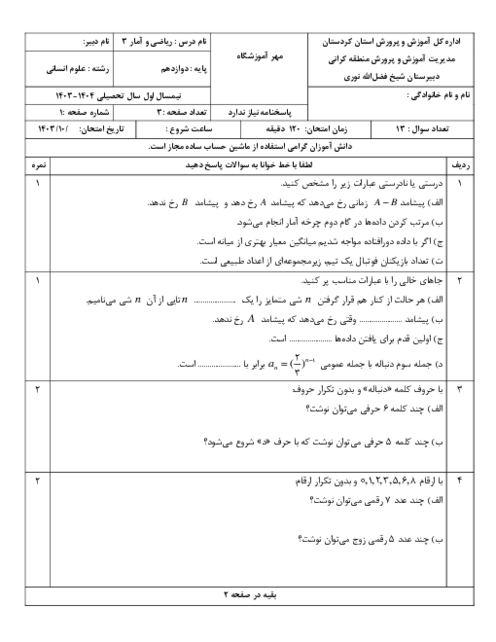
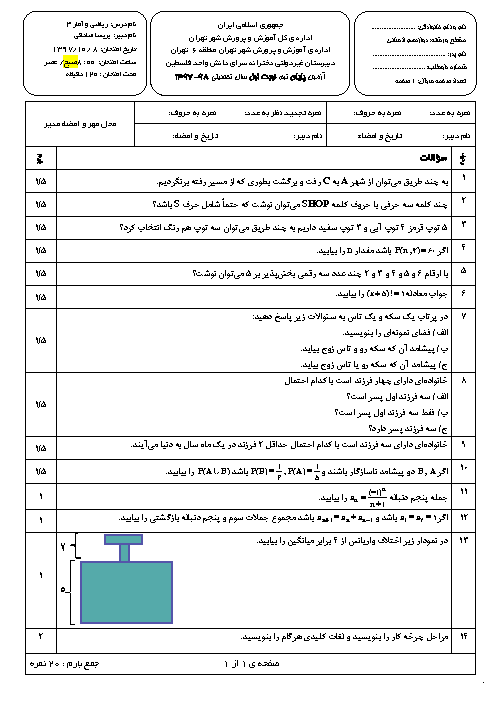
مقدار نقاط داده شده را در تابع جای گذاری می‌کنیم تا $b,a$ را به دست بیاوریم.

  $f\left( x \right)=a{{\left( b \right)}^{x}}-1$

$f\left( -\frac{1}{2} \right)=a{{\left( b \right)}^{-\frac{1}{2}}}-1=a\left( \frac{1}{1} \right)-1=\frac{1}{2}\Rightarrow a\left( \frac{1}{\sqrt{b}} \right)=\frac{1}{2}+1\Rightarrow a\left( \frac{1}{\sqrt{b}} \right)=\frac{3}{2}\begin{matrix}    {} & \left( 1 \right)  \\ \end{matrix}$ 

$f\left( 1 \right)=ab-1=11\Rightarrow ab=12\Rightarrow b=\frac{12}{a}\begin{matrix}    {} & \left( 2 \right)  \\ \end{matrix}$

با جای گذاری (2) در (1) خواهیم داشت:

$a\left( \frac{1}{\sqrt{\frac{12}{a}}} \right)=\frac{3}{2}\Rightarrow \frac{a}{\frac{\sqrt{12}}{\sqrt{a}}}=\frac{3}{2}\Rightarrow \frac{a\sqrt{a}}{\sqrt{12}}=\frac{3}{2}\Rightarrow a\sqrt{a}=\frac{3\times \sqrt{12}}{2}=\frac{3\times 2\sqrt{3}}{2}\Rightarrow a\sqrt{a}=3\sqrt{3}\Rightarrow a=3$ 

$\left( 2 \right)\Rightarrow b=\frac{12}{a}\xrightarrow{a=3}b=4$ 

$f\left( x \right)=3{{\left( 4 \right)}^{x}}-1\Rightarrow f\left( -1 \right)=3\times \frac{1}{4}-1=\frac{3}{4}-\frac{4}{4}=-\frac{1}{4}$