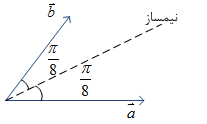
اگر زاویهٔ بین دو بردار $\overrightarrow{a}$ و $\overrightarrow{b}$ برابر $\frac{\pi }{4}$ باشد، زاویهٔ بین دو بردار $\overrightarrow{b}$ و $\left| \overrightarrow{a} \right|\overrightarrow{b}+\left| \overrightarrow{b} \right|\overrightarrow{a}$ کدام است؟
1 )
$\frac{\pi }{4}$
2 )
$\frac{\pi }{3}$
$\frac{\pi }{8}$
4 )
$\frac{3\pi }{8}$
پاسخ تشریحی :
تحلیل ویدئویی تست
محسن ذوالفقاری 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...