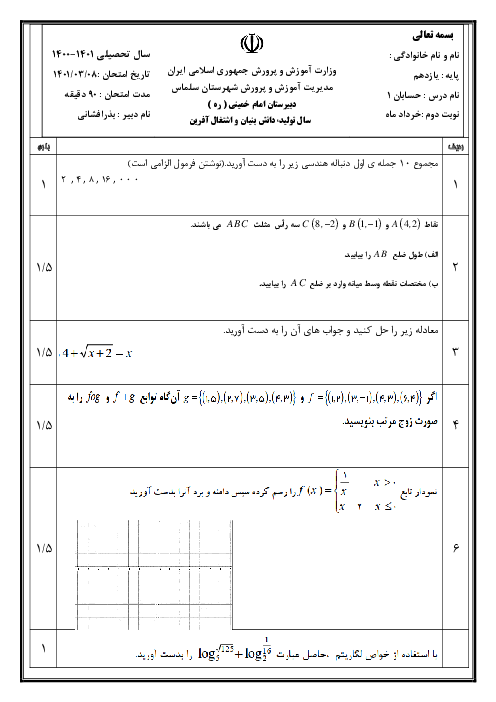
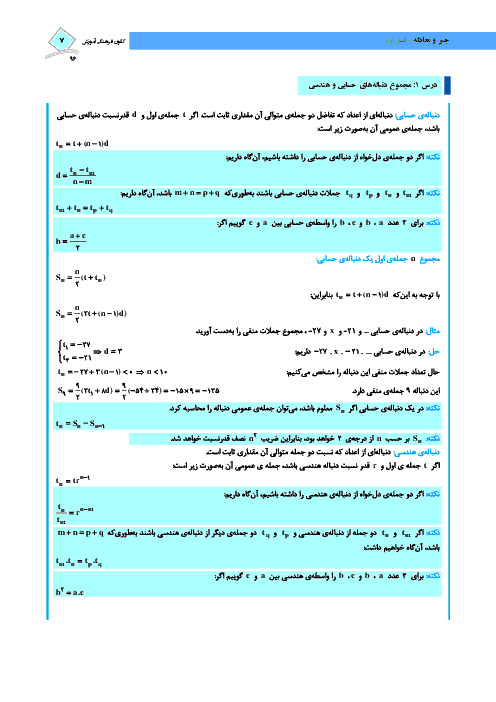
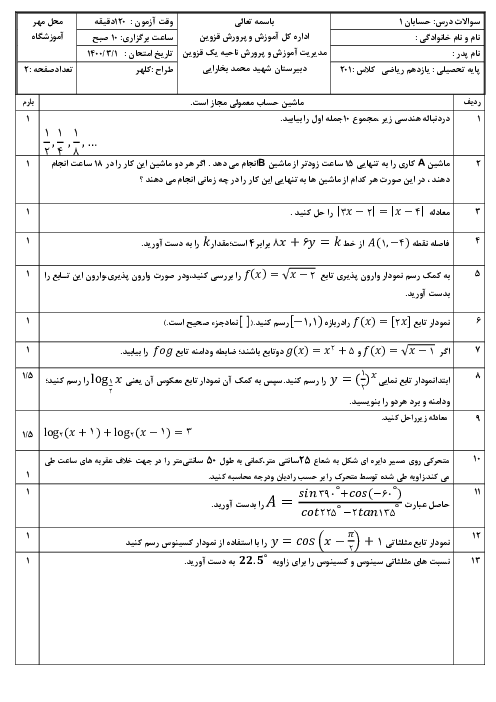
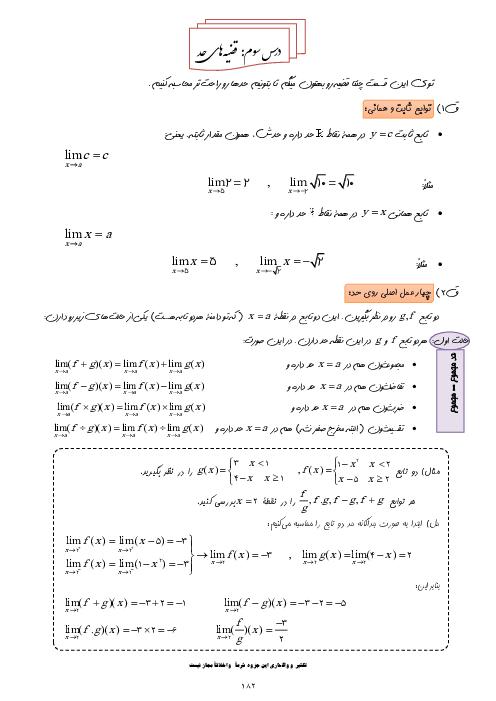
درس 1: مجموع جملات دنباله‌های حسابی و هندسی
حسابان (1)
یازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
اگر در یک دنبالهٔ هندسی، a جملهٔ اول، q قدرنسبت و ${{S}_{n}}$ مجموع n جملهٔ اول باشد، حاصل عبارت $A=\frac{(1-q){{S}_{n}}}{a}+{{q}^{n}}$ کدام است؟ ($q\ne 1$)
تحلیل ویدئویی تست
علی محبیان 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...