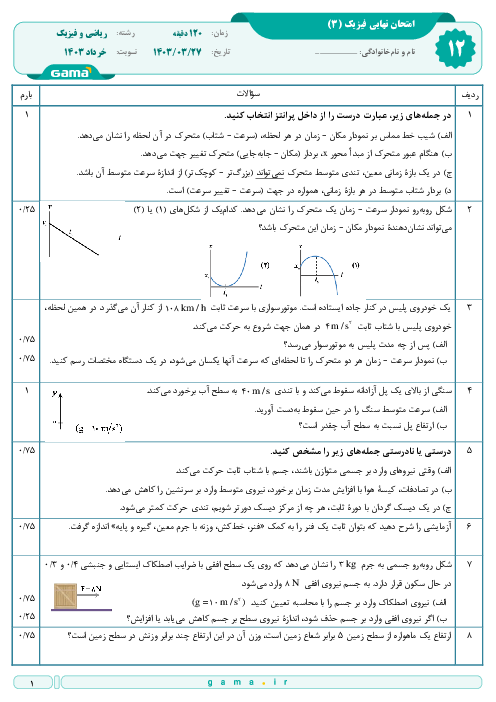
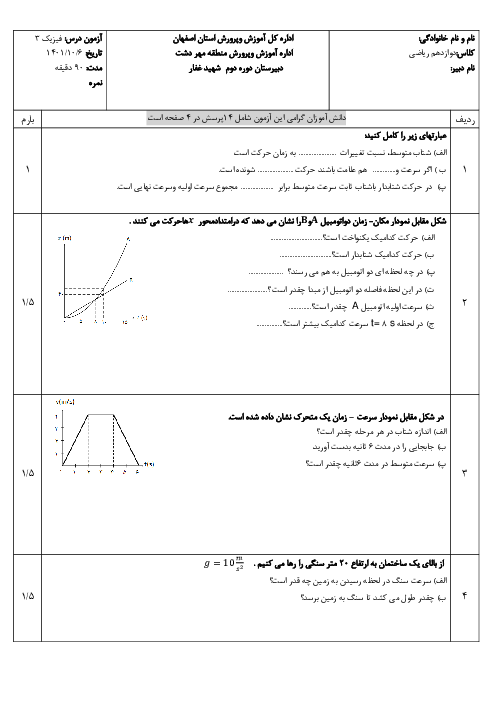
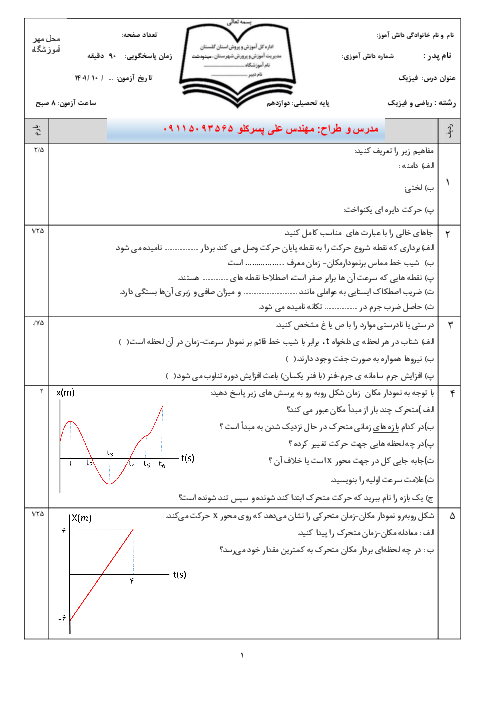
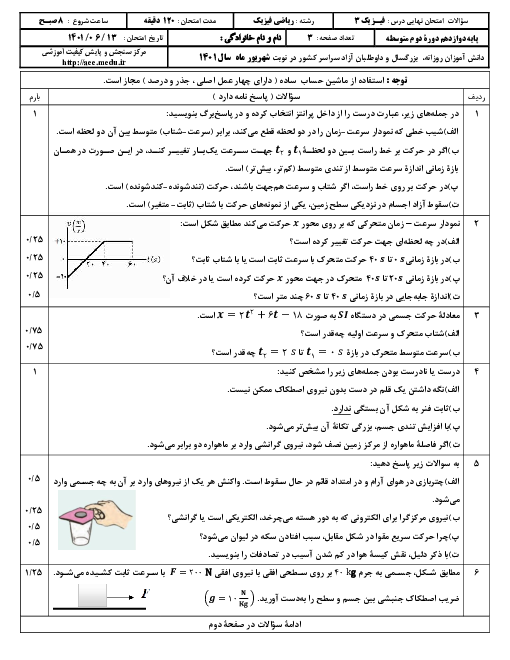
اگر بازۀ زمانی مشخص را $t$ فرض كنيم، تعداد نوسان‌های كامل هر آونگ برابر است با:

$N=\frac{t}{T}\Rightarrow T=\frac{t}{N}\Rightarrow \left\{ \begin{matrix}    {{T}_{A}}=\frac{t}{12}  \\    {{T}_{B}}=\frac{t}{5}  \\ \end{matrix} \right.$

حال با استفاده از رابطۀ دورۀ تناوب آونگ ساده داريم:

$T=2\pi \sqrt{\frac{L}{g}}\Rightarrow L=\frac{{{T}^{2}}g}{4{{\pi }^{2}}}\Rightarrow \left\{ \begin{matrix}    {{L}_{A}}=\frac{T_{A}^{2}g}{4{{\pi }^{2}}}  \\    {{L}_{B}}=\frac{T_{B}^{2}g}{4{{\pi }^{2}}}  \\ \end{matrix} \right.$

${T}'=2\pi \sqrt{\frac{{{L}_{A}}+{{L}_{B}}}{g}}=2\pi \sqrt{\frac{\frac{T_{A}^{2}g}{4{{\pi }^{2}}}+\frac{T_{B}^{2}g}{4{{\pi }^{2}}}}{g}}\Rightarrow {T}'=\sqrt{T_{A}^{2}+T_{B}^{2}}\Rightarrow {T}'=\sqrt{{{\left( \frac{t}{12} \right)}^{2}}+{{\left( \frac{t}{5} \right)}^{2}}}\Rightarrow {T}'=\frac{13t}{60}$

بنابراين تعداد نوسان‌های كامل آونگ جديد برابر است با: 

${N}'=\frac{t}{{{T}'}}=\frac{60}{13}$