درس 1: تبدیل نمودار توابع
حسابان (2)
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
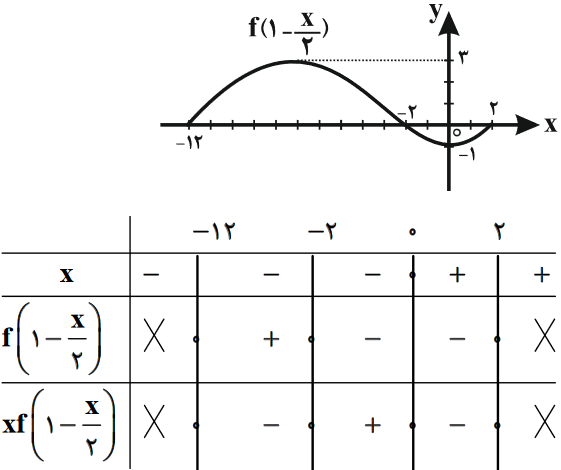
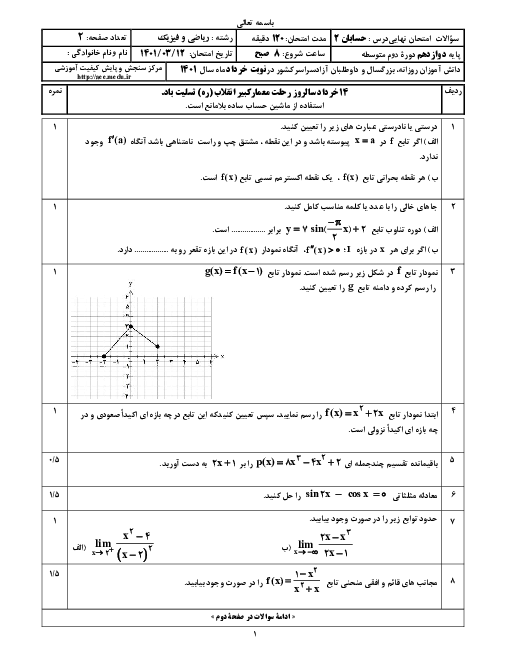
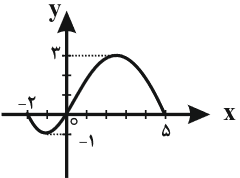
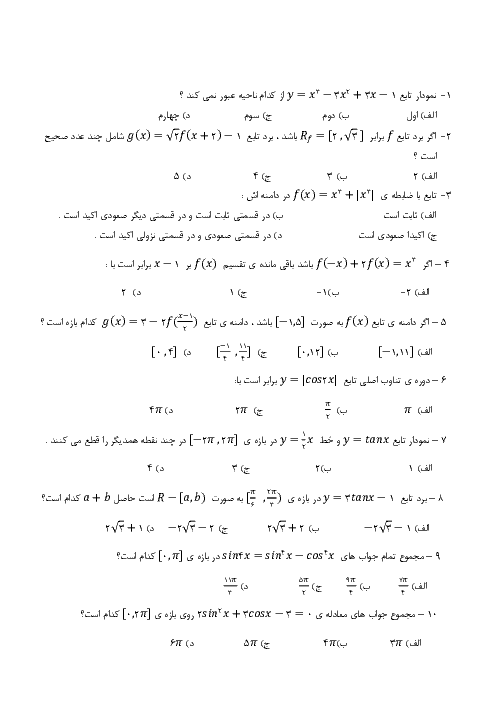اگر نمودار تابع $f(x+2)$ به صورت زیر باشد، دامنهٔ عبارت $\sqrt{xf\left( 1-\frac{x}{2} \right)}$ به کدام صورت است؟
$\left\{ -12,2 \right\}\bigcup \left[ -2,0 \right]$
2 )
$\left[ -12,-2 \right]\bigcup \left[ 0,2 \right]$
3 )
$\left\{ -12 \right\}\bigcup \left[ -2,2 \right]$
4 )
$\left[ -6,-1 \right]\bigcup \left[ 0,1 \right]$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...