توان متوسط انتقال انرژی با مربع دامنه و مربع بسامد موج متناسب است: $\overline{P}\propto {{f}^{2}}{{A}^{2}}$ 

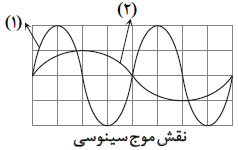
با توجه به شكل، دامنه‌ی موج (۲) نصف دامنه‌ی موج (۱) است. $({{A}_{2}}=\frac{{{A}_{1}}}{2})$ همچنين طول موجِ موج (۲)، دو برابر طول موجِ موج (۱) است. از طرفی چون هر دو موج در يك طناب منتشر می‌شوند، تندی دو موج برابر است $(v=\sqrt{\frac{F}{\mu }})$ به اين ترتيب با توجه به رابطه‌ی $f=\frac{v}{\lambda }$،  بسامد موج (۲) نصف بسامد موج (1) است.  $({{f}_{2}}=\frac{{{f}_{1}}}{2})$ 

$\frac{{{\overline{P}}_{2}}}{{{\overline{P}}_{1}}}={{(\frac{{{f}_{2}}.{{A}_{2}}}{{{f}_{1}}.{{A}_{1}}})}^{2}}={{(\frac{\frac{{{f}_{1}}}{2}.\frac{{{A}_{1}}}{2}}{{{f}_{1}}.{{A}_{1}}})}^{2}}=\frac{1}{16}\Rightarrow \frac{{{\overline{P}}_{2}}}{80}=\frac{1}{16}\Rightarrow {{\overline{P}}_{2}}=5W$