به ازای هر مقدار حقیقی و ناصفر a، تابع روی مشتق‌پذیر است. مقدار ac کدام است؟

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

مشتق و کاربردهای آن ریاضیات کنکور سراسری دوره دوم متوسطه- نظری علوم ریاضی

به ازای هر مقدار حقیقی و ناصفر a، تابع $f(x) = \left\{ \begin{gathered}
\begin{array}{*{20}{c}}
{bx + c}&{x < a}
\end{array} \hfill \\
\begin{array}{*{20}{c}}
{\frac{1}{x}}&{x \geqslant a}
\end{array} \hfill \\
\end{gathered} \right.$ روی $\mathbb{R}$ مشتق‌پذیر است. مقدار ac کدام است؟

1 )

2 )

3 )

4 )

نمایش پاسخ

تابع باید در $x = a$ نیز مشتق‌پذیر باشد، پس در این نقطه در ابتدا باید پیوسطه باشد.

$\mathop {\lim }\limits_{x \to {a^ - }} f(x) = ab + c,\mathop {\lim }\limits_{x \to {a^ + }} f(x) = \frac{1}{a} = f(a)$
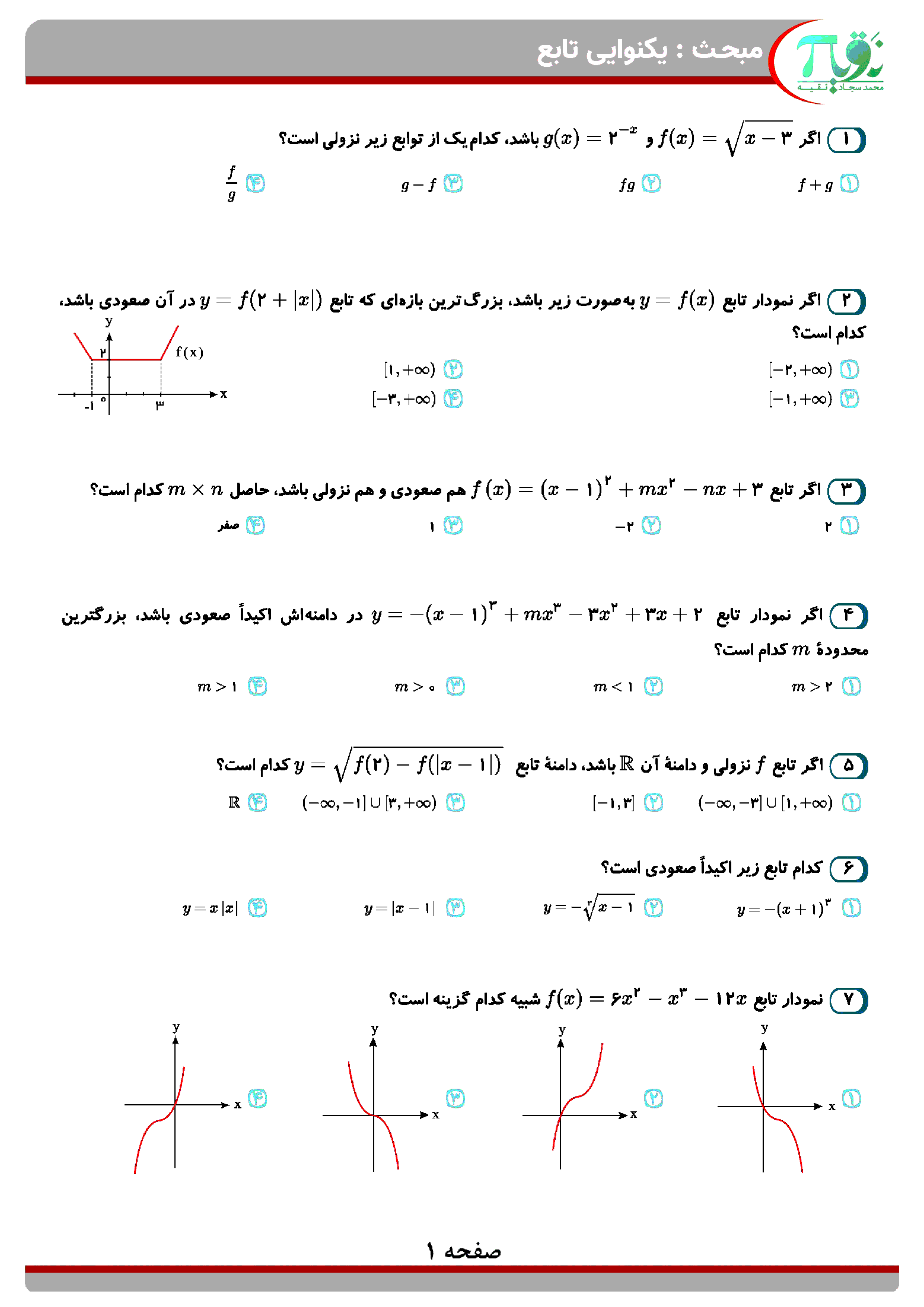
$\begin{array}{*{20}{c}}
{ \to ab + c = \frac{1}{a}}&{( * )}
\end{array}$

تابع مشتق را به دست می‌آوریم:

$f'(x) = \left\{ \begin{gathered}
\begin{array}{*{20}{c}}
b&{x < a}
\end{array} \hfill \\
\begin{array}{*{20}{c}}
{ - \frac{1}{{{x^2}}}}&{x \geqslant a}
\end{array} \hfill \\
\end{gathered} \right. \Rightarrow {{f'}_ - }(a) = b,{{f'}_ + }(a) = - \frac{1}{{{a^2}}}$

مشتق‌های چپ و راست نیز باید با هم برابر باشند:

$b = - \frac{1}{{{a^2}}}\xrightarrow{{\left( * \right)}}a( - \frac{1}{{{a^2}}}) + c = \frac{1}{a} \Rightarrow c = \frac{2}{a} \Rightarrow ac = 2$

گزارش اشکال