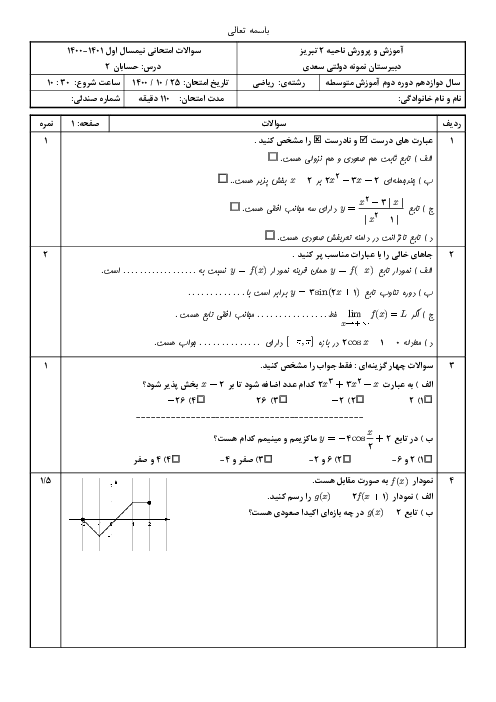
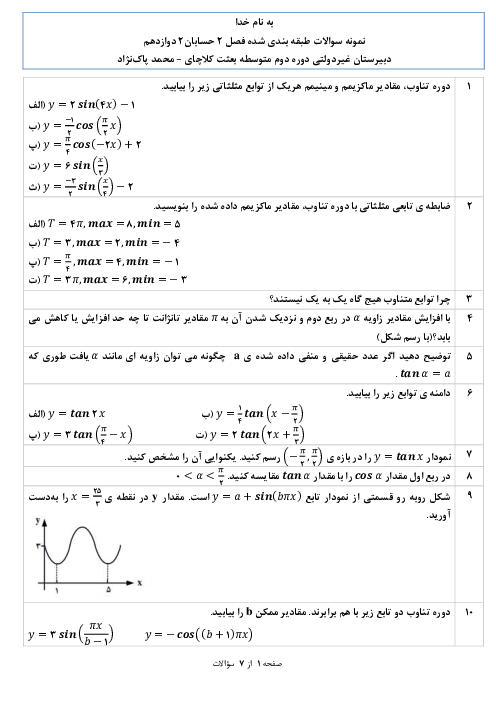
درس 1: اکسترممهای یک تابع و توابع صعودی و نزولی
حسابان (2)
دوازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
سطح جانبی یک استوانه $S'$ و سطح قاعدهٔ آن $S$ است. اگر $S+S'=12$ فرض شود، شعاع قاعدهٔ استوانه چقدر باشد تا حجم ماکزیمم گردد؟
1 )
$\frac{2}{\pi }$
2 )
$\frac{3}{\pi }$
$\frac{2}{\sqrt{\pi }}$
4 )
$\frac{3}{\sqrt{\pi }}$