متحرک با سرعت ثابت در جهت محور در حال حرکت است و در لحظه‌ای که به فاصله‌ی 150 متری متحرک می‌رسد، متحرک با شتاب ثابت در جهت محور شروع به حرکت می‌کند. کم‌ترین… | فیزیک (3) تجربی دوازدهم شماره 75193

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

قسمت 2: حرکت با سرعت ثابت فیزیک (3) تجربی دوازدهم دوره دوم متوسطه- نظری علوم تجربی درسنامه آموزشی این مبحث

متحرک $A$ با سرعت ثابت $72\frac{km}{h}$ در جهت محور $x$ در حال حرکت است و در لحظه‌ای که به فاصله‌ی 150 متری متحرک $B$ می‌رسد، متحرک $B$ با شتاب ثابت $2\frac{m}{{{s}^{2}}}$ در جهت محور $x$ شروع به حرکت می‌کند. کم‌ترین فاصله‌ی بین این دو متحرک چند متر است؟

1 )

100

2 )

3 )

4 )

نمایش پاسخ

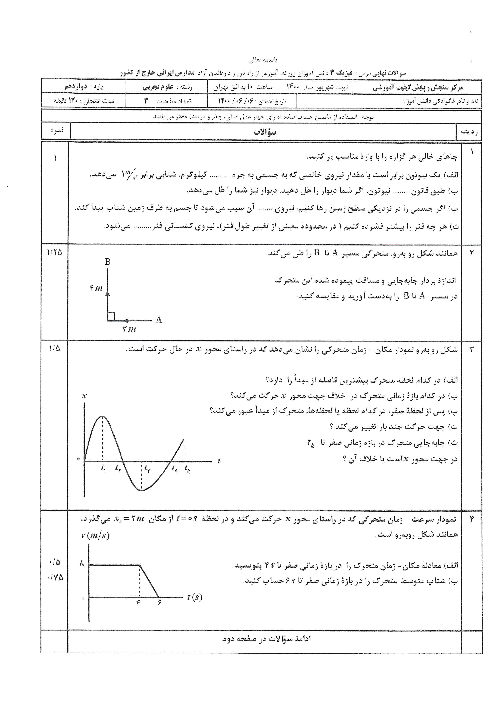
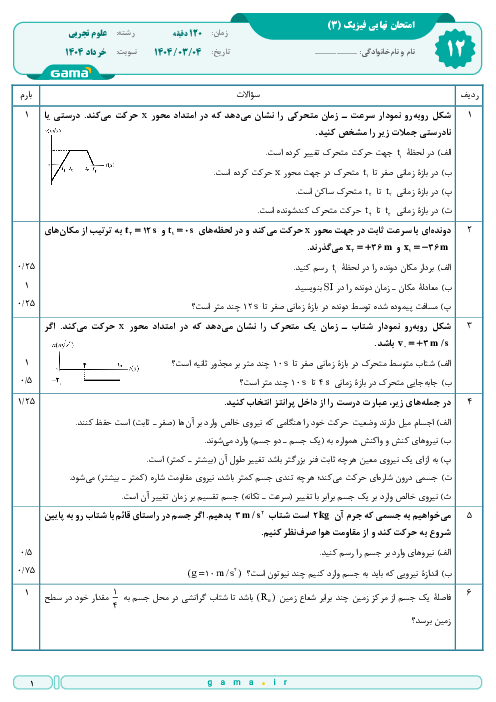
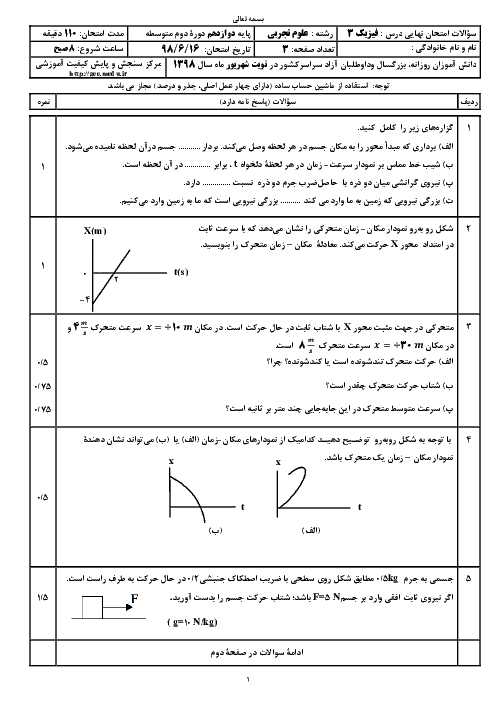
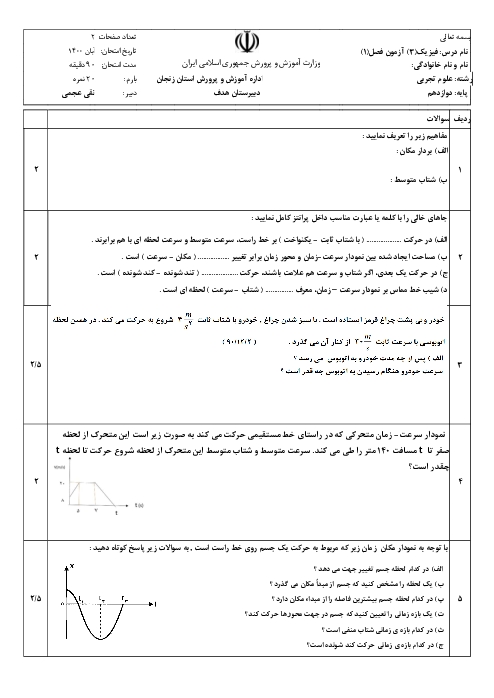
لحظه‌ای که متحرک $A$ به فاصله‌ی 150 متری متحرک $B$ می‌رسد را ${{t}_{{}^\circ }}=0$ فرض می‌کنیم و مکان متحرک $A$ را در این لحظه مبدأ مختصات محور $x$ فرض می‌کنیم. معادله‌ی حرکت دو متحرک را می‌نویسیم:

${{v}_{A}}=\frac{72}{3/6}\frac{m}{s}=20\frac{m}{s}$

${{x}_{A}}={{v}_{A}}t+{{x}_{{}^\circ }}\Rightarrow {{x}_{A}}=20t$

${{x}_{B}}=\frac{1}{2}{{a}_{B}}{{t}^{2}}+{{v}_{{}^\circ B}}t+{{x}_{{}^\circ B}}\Rightarrow {{x}_{B}}={{t}^{2}}+150$

برای محاسبه‌ی فاصله‌ی بین دو متحرک می‌توان نوشت:

${{x}_{B}}-{{x}_{A}}={{t}^{2}}+150-20t={{t}^{2}}-20t+100+50={{(t-10)}^{2}}+50$

حداقل مقدار ${{(t-10)}^{2}}$ برابر صفر است$(t=10s)$، بنابراین کم‌ترین مقدار ${{x}_{B}}-{{x}_{A}}$ (فاصله‌ی بین دو متحرک) برابر $50m$ می‌باشد.

گزارش اشکال