دامنهٔ نوسان نوسانگر ساده‌ای 4 سانتی‌متر است. اگر نوسانگر در لحظهٔ در فاصلهٔ 2+ سانتی‌متری مبدأ باشد، معادلهٔ حرکت آن در کدام گزینه می‌تواند باشد؟ | فیزیک (3) ریاضی دوازدهم شماره 67016

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

قسمت 2: حرکت هماهنگ ساده فیزیک (3) ریاضی دوازدهم دوره دوم متوسطه- نظری علوم ریاضی درسنامه آموزشی این مبحث

دامنهٔ نوسان نوسانگر ساده‌ای 4 سانتی‌متر است. اگر نوسانگر در لحظهٔ $t=\frac{1}{180}s$ در فاصلهٔ 2+ سانتی‌متری مبدأ باشد، معادلهٔ حرکت آن در $SI$ کدام گزینه می‌تواند باشد؟

1 )

$x=0/04\cos (30\pi t)$

2 )

$x=0/04\cos (60\pi t)$

3 )

$x=0/04\cos (300\pi t)$

4 )

گزینه‌های (2) و (3) می‌تواند صحیح باشد.

نمایش پاسخ

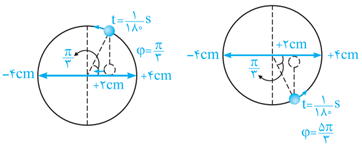
فرم کلی معادلهٔ مکان - زمان را به صورت رابطهٔ $x=A\cos \omega t$ در نظر می‌گیریم. با توجه به صورت سؤال، دامنهٔ حرکت برابر $4cm$ یا $0/04m$ است و برای نوشتن معادلهٔ مکان - زمان، کافی است $\omega $ را به دست آوریم. این نوسانگر در $t=\frac{1}{180}s$ در مکان $x=+2cm$ قرار دارد و $\omega $ برای آن به‌صورت زیر محاسبه می‌شود:

$\cos \varphi =\frac{x}{A}=\frac{+2}{4}=+\frac{1}{2}\Rightarrow \varphi =\frac{\pi }{3}$ یا $\frac{5\pi }{3}$

اگر فاز حرکت در لحظهٔ $t=\frac{1}{180}s$ برابر $\frac{\pi }{3}$ باشد:

$\varphi =\omega t\Rightarrow \frac{\pi }{3}=\omega \times \frac{1}{180}\Rightarrow \omega =60\pi {rad}/{s}\;$

اگر فاز حرکت در لحظهٔ $t=\frac{1}{180}s$ برابر $\frac{5\pi }{3}$ باشد:

$\varphi =\omega t\Rightarrow \frac{5\pi }{3}=\omega \times \frac{1}{180}\Rightarrow \omega =300\pi rad/s\ $