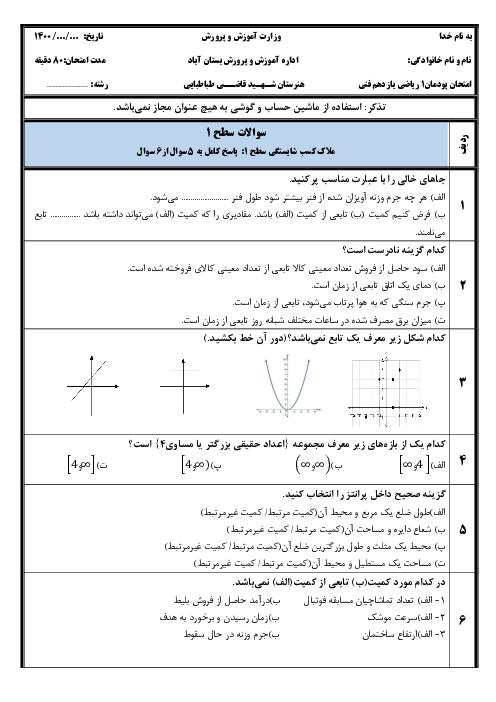
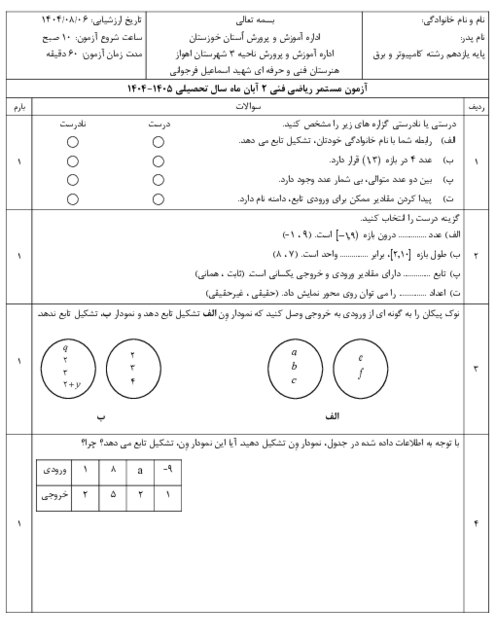
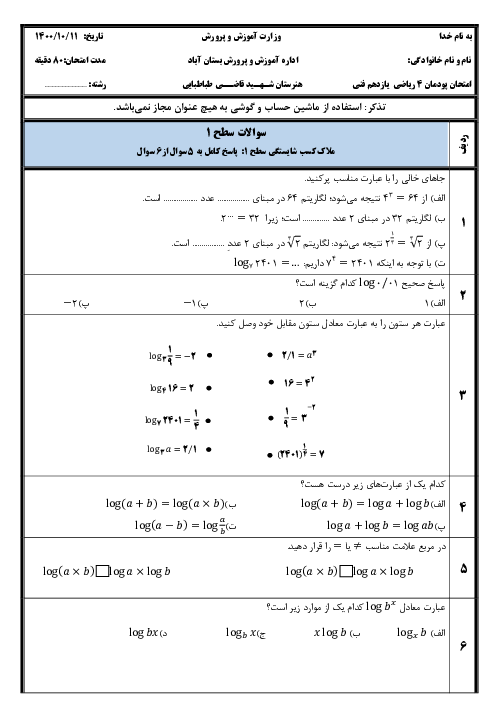
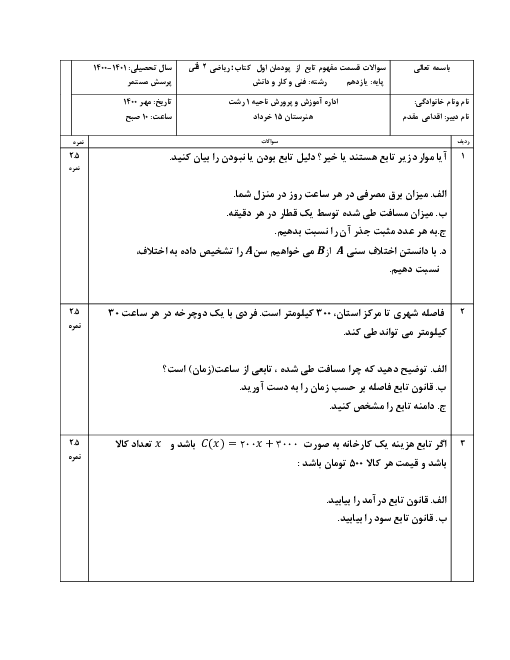
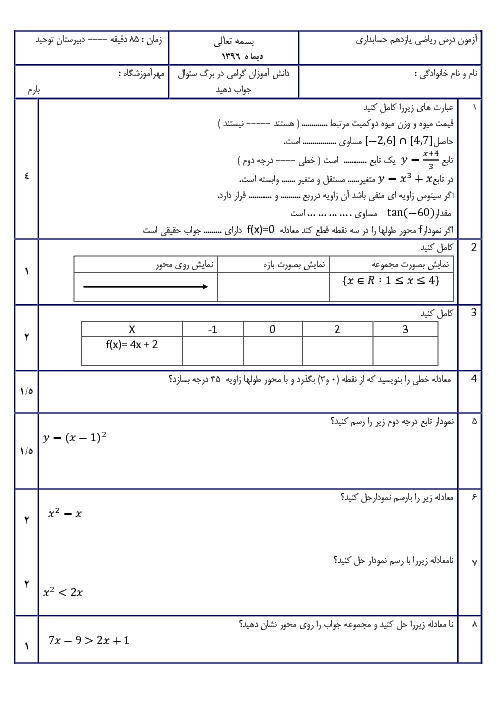
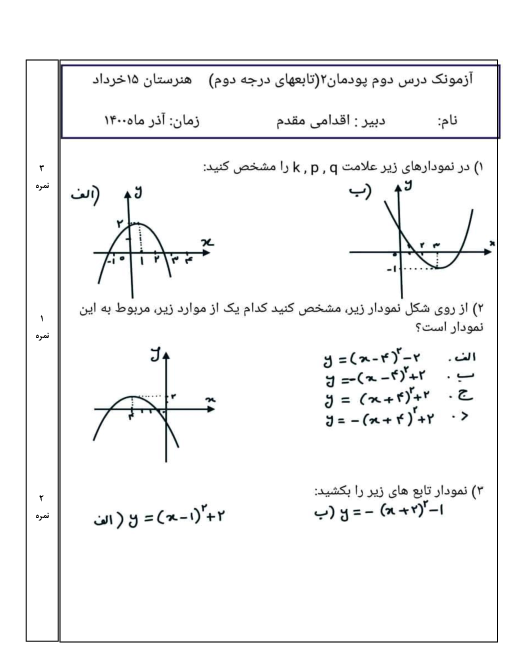
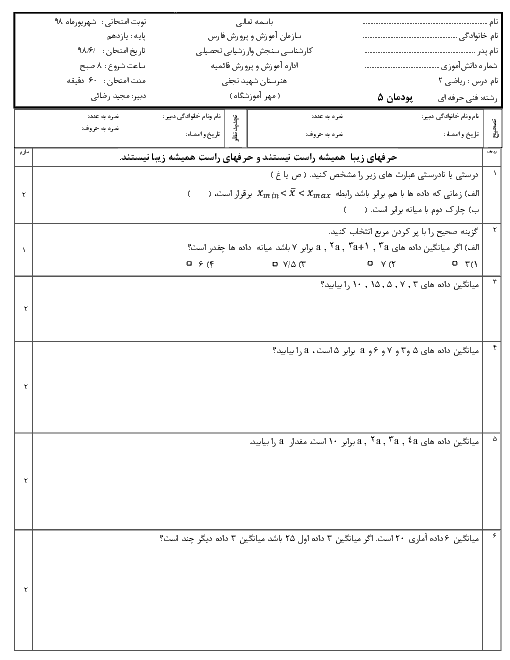
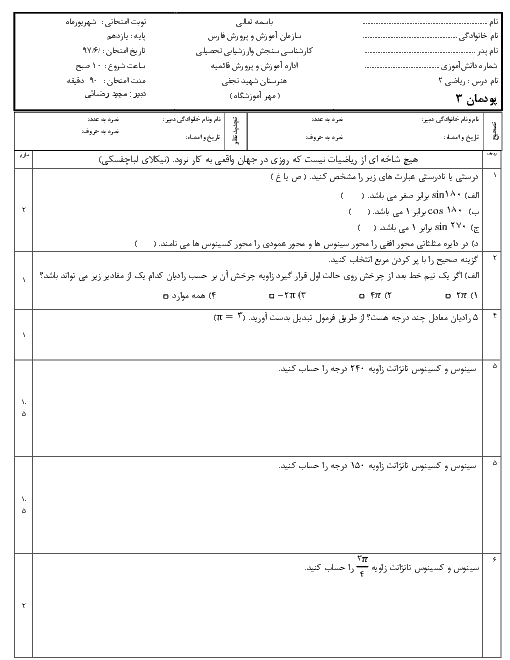
پودمان 3: زاویههای دلخواه و نسبتهای مثلثاتی آنها
ریاضی2 فنی
یازدهم
متوسطه دوم فنی
مشترک شاخۀ فنی و حرفهای
درسنامه آموزشی این مبحث
اگر $\tan \theta =0/2$ باشد، مقدار $A=\frac{-\sin \left( 2\pi -\theta \right)-\cos \left( \pi +\theta \right)}{\sin \left( \pi -\theta \right)-\sin \left( 2\pi +\theta \right)}$ کدام است؟
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!