درس 5: آشنایی با هندسه تحلیلی
حسابان (1)
یازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
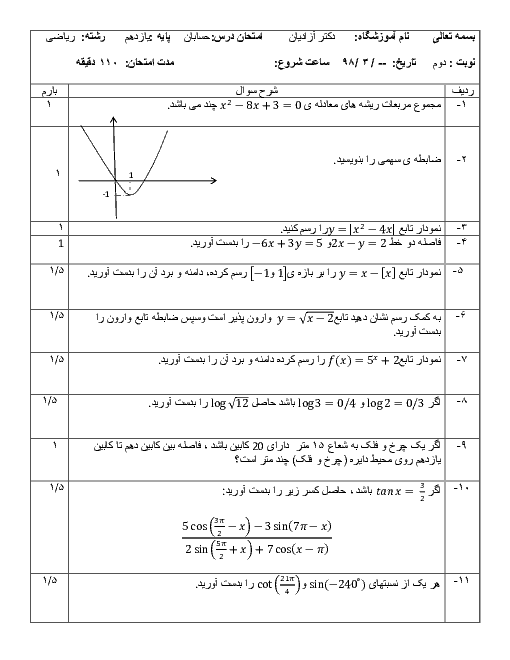
$M$ نقطه‌ای دلخواه روی خط $y=3-2x$ است. فاصلهٔ $M$ تا خط $3x-4y=8$ را به صورت تابعی از طول نقطهٔ $M$ نوشته‌ایم. ضابطهٔ این تابع کدام است؟
1 )
$f(x)=\frac{1}{25}\left| 11x-20 \right|$
2 )
$f(x)=\frac{1}{5}\left| 5x-4 \right|$
3 )
$f(x)=\frac{1}{25}\left| 5x-4 \right|$
$f(x)=\frac{1}{5}\left| 11x-20 \right|$
پاسخ تشریحی :
تحلیل ویدئویی تست
علی محبیان 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...