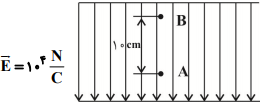
در ابتدا بار ذرهٔ باردار را می‌یابیم. شرط تعادل این است که نیروی میدان الکتریکی وزن جسم را خنثی کند، بنابراین داریم:

$F=E\left| q \right|$

$\underset{\downarrow \overrightarrow{mg}}{\overset{\uparrow \overrightarrow{F}}{\mathop{\bigcirc }}}\,\to E\left| q \right|=mg\xrightarrow[m=10\times {{10}^{-3}}kg]{E={{10}^{4}}\frac{N}{C}}$

$({{10}^{4}})\left| q \right|=10\times {{10}^{-3}}\times 10\Rightarrow \left| q \right|={{10}^{-5}}C$

از طرفی چون نیروی میدان الکتریکی در خلاف جهت خط‌های میدان است بار ذره منفی است. حال برای تعیین چگونگی تغییر انرژی پتانسیل الکتریکی ذره، چون بار منفی در خلاف جهت خط‌های میدان جابه‌جا می‌شود، انرژی پتانسیل الکتریکی‌اش کاهش می‌یابد. برای تعیین مقدار این کاهش داریم:

$\left| \Delta U \right|=\left| q \right|Ed={{10}^{-5}}\times {{10}^{4}}\times 0/1\Rightarrow \left| \Delta U \right|=0/01J$

چون انرژی پتانسیل الکتریکی کاهش یافته داریم: $\Delta U=-0/01J$