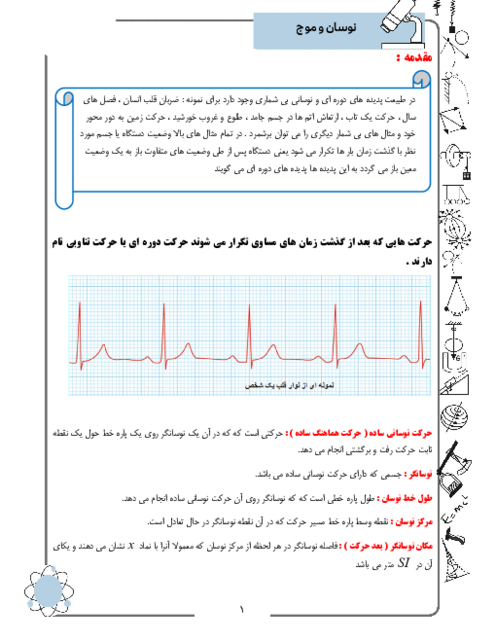
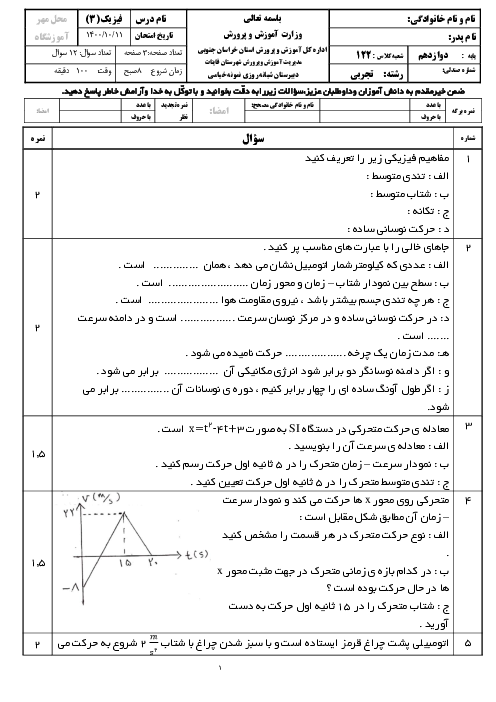
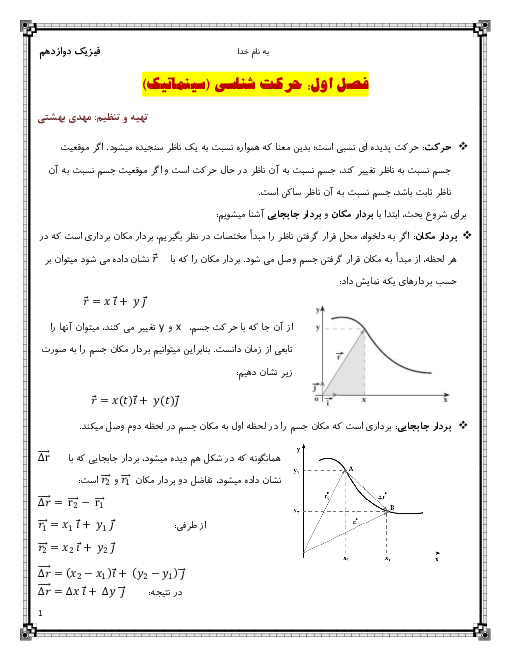
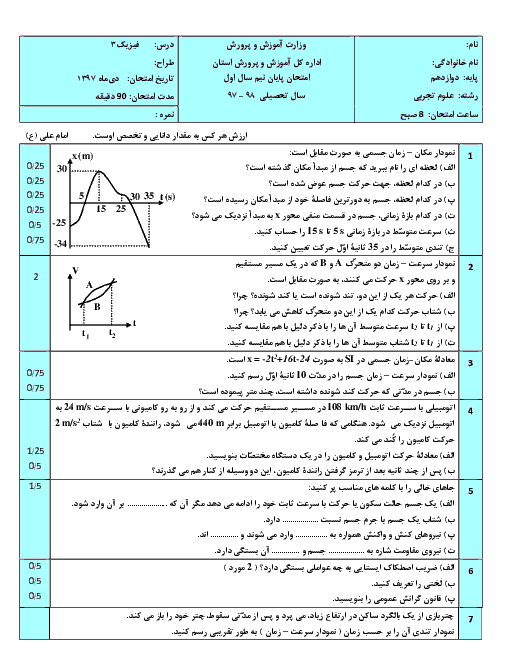
حرکت جزء $M$ (یا هر جزء دیگری از طناب) به‌صورت حرکت هماهنگ ساده است معادلهٔ حرکت آن معادلهٔ هماهنگ ساده یعنی $y=A\cos \omega t$ است. در لحظه‌ای که شکل نشان می‌دهد جزء $M$ در حال عبور از نقطهٔ تعادل خود است ($y=0$) و با توجه به جهت انتشار موج، این نقطه با دریافت حرکت نقطهٔ ماقبل خود در حال حرکت به‌طرف بالاست و برای این منظور باید شناسهٔ کسینوس آن $\frac{3\pi }{2}$ باشد. وقتی با گذشت زمان و برای اولین بار ذره به $y=+\frac{A}{2}$ می‌رسد، باید شناسهٔ کسینوس به $\frac{5\pi }{3}$ برسد و داریم:

$\left\{ \begin{align}  & 0=A\cos \omega {{t}_{1}} \\  & +\frac{A}{2}=A\cos \omega {{t}_{2}} \\ \end{align} \right.$

$\Rightarrow \left\{ \begin{align}  & \cos \frac{3\pi }{2}=\cos \omega {{t}_{1}} \\  & \cos \frac{5\pi }{3}=\cos \omega {{t}_{2}} \\ \end{align} \right.$

$\Rightarrow \left\{ \begin{align}  & \omega {{t}_{1}}=\frac{3\pi }{2} \\  & \omega {{t}_{2}}=\frac{5\pi }{3} \\ \end{align} \right.\Rightarrow \omega ({{t}_{2}}-{{t}_{1}})=\frac{5\pi }{3}-\frac{3\pi }{2}\Rightarrow 2\pi f\Delta t=\frac{\pi }{6}$

$\begin{align}  & 2\pi \times 100\times \Delta t=\frac{\pi }{6}\Rightarrow \Delta t=\frac{1}{1200}s \\  & \Rightarrow v=\frac{\Delta x}{\Delta t}=\frac{0/1}{\frac{1}{1200}}=120\frac{m}{s} \\ \end{align}$