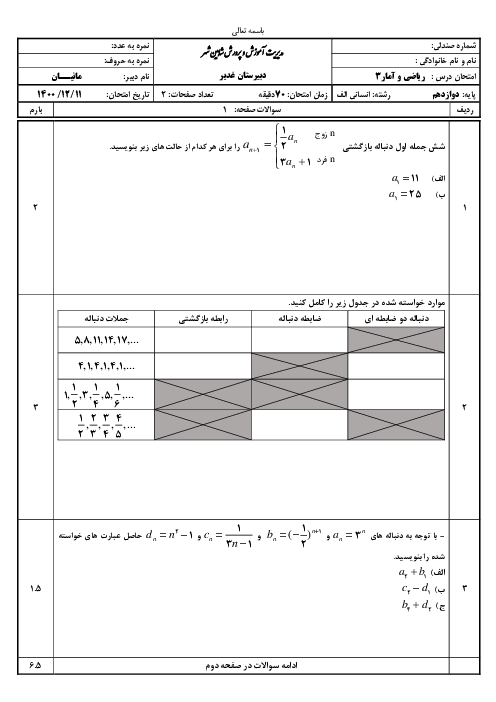
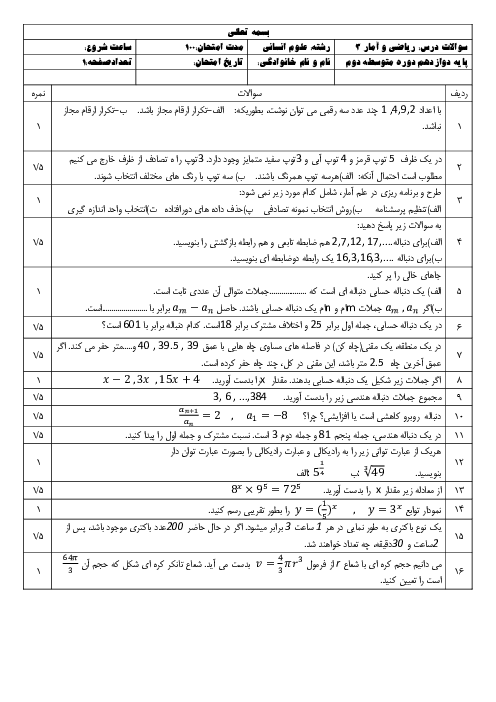
چرا با وجود اینکه صورت سوال گفته است مجموع جملات از فرمول مجموع استفاده نکردیم؟ به این دلیل که مجموع جملات همیشه، مجموع چند جمله از اول است که برای مجموع جملات اول و دوم که در صورت سوال گفته است می‌توان نوشت ولی برای مجموع جملات سوم و چهارم نمی‌شود از ان فرمول استفاده کرد، چرا که مجموع $n$ جمله اول نیست و از وسط جملات شروع شده است. پس به جای آن خود جملات را می‌نویسیم و بعد باز می‌کنیم و بعد چون «دو معادلۀ دو مجهولی» داریم از طریق دستگاه حل می‌کنیم.

${{a}_{n}}=a{{r}^{n-1}}$ 

$\left\{ \begin{matrix}    {{a}_{1}}+{{a}_{2}}=\frac{9}{2}\Rightarrow {{a}_{1}}+{{a}_{1}}r=\frac{9}{2}\Rightarrow {{a}_{1}}\left( 1+r \right)=\frac{9}{2}  \\    {{a}_{4}}+{{a}_{5}}=36\Rightarrow {{a}_{1}}{{r}^{3}}+{{a}_{1}}{{r}^{4}}=36\Rightarrow {{a}_{1}}{{r}^{3}}\left( 1+r \right)=36  \\ \end{matrix} \right.$ 

طرفین تساوی را بر هم تقسیم می‌کنیم $\Rightarrow \frac{{{a}_{1}}\left( 1+r \right)}{{{a}_{1}}{{r}^{3}}\left( 1+r \right)}=\frac{\frac{9}{2}}{36}\Rightarrow \frac{1}{{{r}^{3}}}=\frac{1}{8}\Rightarrow {{r}^{3}}=8\Rightarrow r=2$ 

${{a}_{1}}\left( 1+2 \right)=\frac{9}{2}\Rightarrow {{a}_{1}}=\frac{9}{6}=\frac{3}{2}\Rightarrow {{a}_{3}}={{a}_{1}}{{r}^{2}}=\frac{3}{2}{{\left( 2 \right)}^{2}}=6$