نمودار تابع با دامنهٔ کدام است؟ | ریاضی (2) یازدهم شماره 47395 - گاما

گاما رو نصب کن!

درحال دریافت اطلاعات ...

{{ successMsg }}

{{ errorMsg }}

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

ورود با رمزعبور

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

نوبت اول گام به گام کاربرگ آزمون عملکردی پودمان آزمون پیشرفت تحصیلی طرح درس نمونه سوال تست پاورپوینت علوم هشتم فارسی چهارم ریاضی هفتم علوم نهم گزارش کارورزی

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

فرم معتبر نیست.

درس 1: آشنایی با برخی از انواع توابع ریاضی (2) یازدهم دوره دوم متوسطه- نظری علوم تجربی درسنامه آموزشی این مبحث

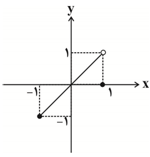
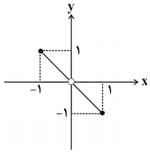
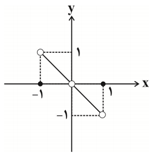
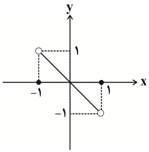
نمودار تابع $y=x(\left[ -x \right]+\left[ x \right])$ با دامنهٔ $-1\le x\le 1$ کدام است؟

1 )

2 )

3 )

4 )

نمایش پاسخ

روش اول: عدد گذاری:

$x=1\to y=1(\left[ -1 \right]+\left[ 1 \right])=1\times ()=0$

$x=0\Rightarrow y=0$

$x=-1\Rightarrow y=0$

يعنی تابع در سه نقطهٔ دلخواهی كه داديم مقداری برابر صفر دارد كه اين سه نقطه فقط در نمودار گزينهٔ 4 صدق می‌كند. روش دوم:

نکته: $y=\left[ x \right]+\left[ -x \right]=\left\{ \begin{matrix} -1,x\notin Z \\ 0,x\in Z \\ \end{matrix} \right.$

$\Rightarrow \left\{ \begin{matrix} -1\lt x\lt 1\xrightarrow[x\notin Z]{x\ne 0}y=-x \\ x=-1,0,1\Rightarrow y=0 \\ \end{matrix} \right.$

تابع رسم شده در گزینهٔ 4 در نقاط 1، 0 و $x=-1$ مقداری برابر صفر دارد و در $-1\lt x\lt 1$ برابر $y=-x$ است.

گزارش اشکال

یک تست دیگه بزن

یک آزمون کامل بده

تحلیل ویدئویی تست

1401/04/16

یوسف شاکر اردکانی

ویدیو دوره آموزشی، ریاضی (2) یازدهم دوره دوم متوسطه- نظری

مدرس: محمد ابراهیمی علویجه

مدت دوره: 26 ساعت (38 فایل)

با گنجینه سوال، آزمون دلخواهتو بساز

ترند شده

بسته ویژه نمره بیست: 5 نمونه سوال شبه نهایی ریاضی (2) یازدهم تجربی

23 صفحه

بسته ویژه نمره بیست: 5 نمونه سوال شبه نهایی ریاضی (2) یازدهم تجربی

ويژه نامه نوبت اول و…

سوپراستار

بسته ویژه نمره بیست: 5 نمونه سوال شبه نهایی ریاضی (2) یازدهم تجربی

23 صفحه

بسته ویژه نمره بیست: 5 نمونه سوال شبه نهایی ریاضی (2) یازدهم تجربی

ويژه نامه نوبت اول و…

سوپراستار

9 سری آزمون نوبت اول ریاضی (2) یازدهم تجربی دبیرستان سادات موسوی | دی 1399

18 صفحه

9 سری آزمون نوبت اول ریاضی (2) یازدهم تجربی دبیرستان سادات موسوی | دی…

داوود شهریاری

رایـــــگان

سوالات امتحان ریاضی (2) پایه یازدهم رشتۀ تجربی دبیرستان پاسداران قزوین | فصل 1 و 2

2 صفحه

سوالات امتحان ریاضی (2) پایه یازدهم رشتۀ تجربی دبیرستان پاسداران قزوین…

حسن کلهر

مجموعه سوالات پاسخ دار ریاضی (2) یازدهم | فصل 7: آمار و احتمال

9 صفحه

مجموعه سوالات پاسخ دار ریاضی (2) یازدهم | فصل 7: آمار و احتمال

علی فقیهی

رایـــــگان

سؤالات تستی ریاضی (2) یازدهم رشته تجربی + جواب | محاسبۀ حد

13 صفحه

سؤالات تستی ریاضی (2) یازدهم رشته تجربی + جواب | محاسبۀ حد

سید حسین رضوی

رایـــــگان

سوالات امتحان ریاضی (2) یازدهم رشته تجربی دبیرستان حافظ | فصل 4 و 5

1 صفحه

سوالات امتحان ریاضی (2) یازدهم رشته تجربی دبیرستان حافظ | فصل 4 و 5

سید امید حسینی

رایـــــگان

نمونه سوال آمادگی امتحان نوبت اول ریاضی (2) رشتۀ تجربی پایۀ یازدهم منطقۀ کردکوی

2 صفحه

نمونه سوال آمادگی امتحان نوبت اول ریاضی (2) رشتۀ تجربی پایۀ یازدهم منطقۀ…

مسلم آقازاده

نمونه سوال امتحان نوبت اول ریاضی 2 دبیرستان شاهد وارثان حسین | تا پایان ص. 76

6 صفحه

نمونه سوال امتحان نوبت اول ریاضی 2 دبیرستان شاهد وارثان حسین | تا پایان…

علیرضا شریفی

رایـــــگان

امتحان ریاضی (2) تجربی یازدهم رشته تجربی دبیرستان اسری مهاباد | مثلثات و تابع نمایی

1 صفحه

امتحان ریاضی (2) تجربی یازدهم رشته تجربی دبیرستان اسری مهاباد | مثلثات…

کاوه عباس نژاد

موارد بیشتر

موارد بیشتر

ارسال فایل

در هر مورد با عوض کردن جای فرض و حکم عکس ‌آنچه را داده شده است، بنویسید.

کدام دسته از داده‌های روبرو داده‌های بهتر و قابل اعتمادتری هستند؟

معادله داده شده چند جواب دارد؟؟ ${x^2} - 2x + 1 = \sqrt { - x + 2} $

موارد بیشتر

ارسال پرسش

موارد بیشتر