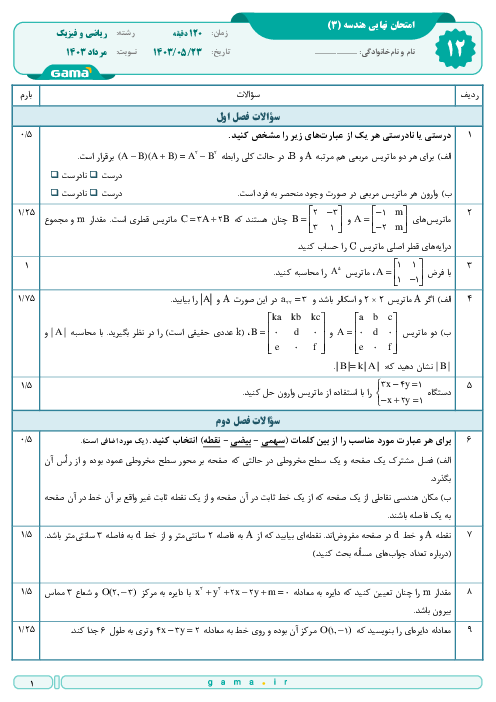
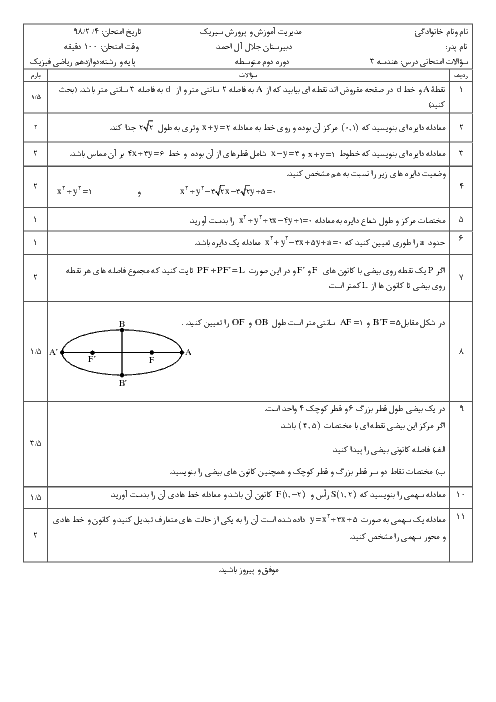
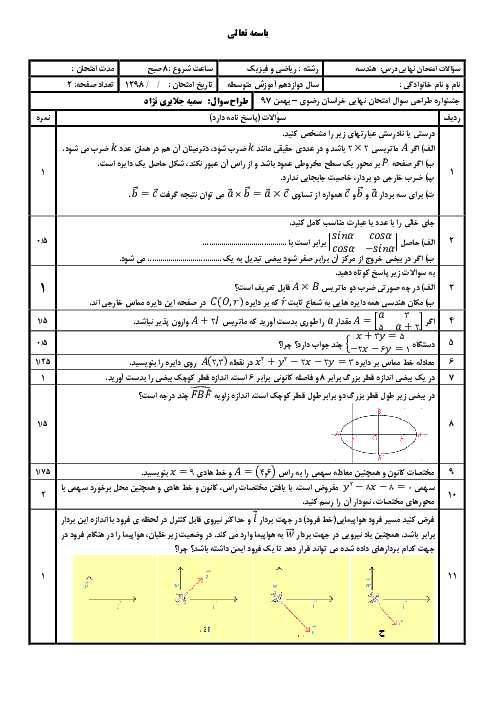
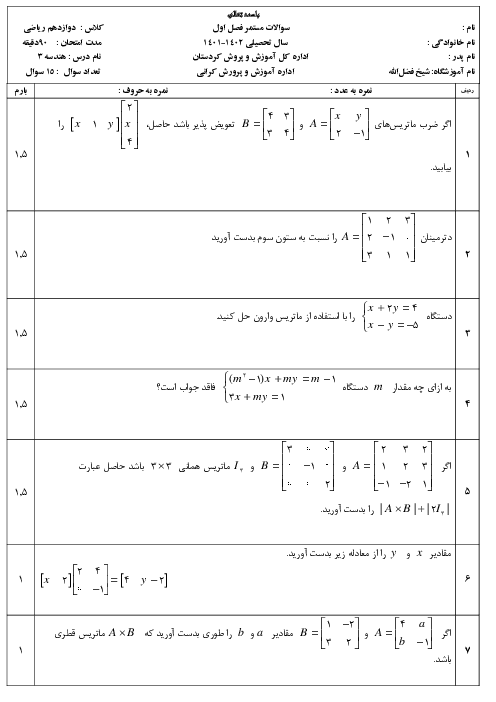
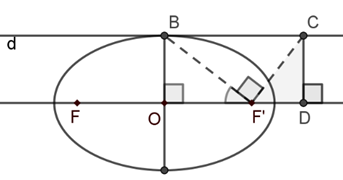
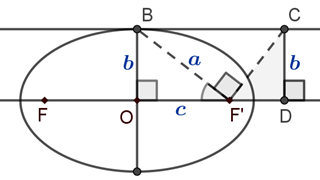
خروج از مرکز بیضی زیر برابر $\frac{{\sqrt 2 }}{2}$ و قطر کوچک آن 2 است. خط d از نقطهٔ B موازی قطر بزرگ بیضی رسم شده است و پاره‌خط‌های $F'C$ و $BF'$ بر هم عمود هستند. پاره‌خط CD موازی قطر کوچک بیضی رسم شده است.
الف) زاویهٔ $\widehat {BF'O}$ چند درجه است؟
ب) مساحت مثلث $F'CD$ را به دست آورید.
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...