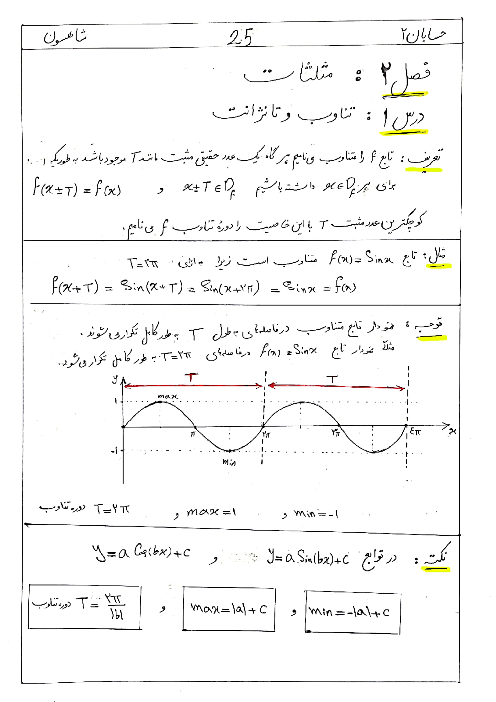
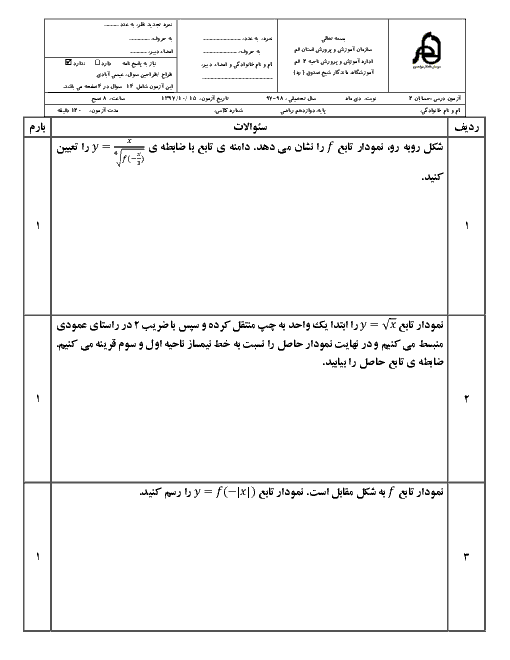
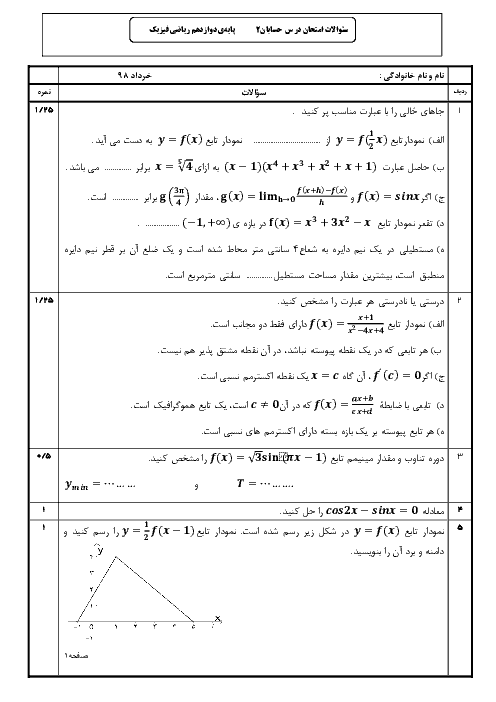
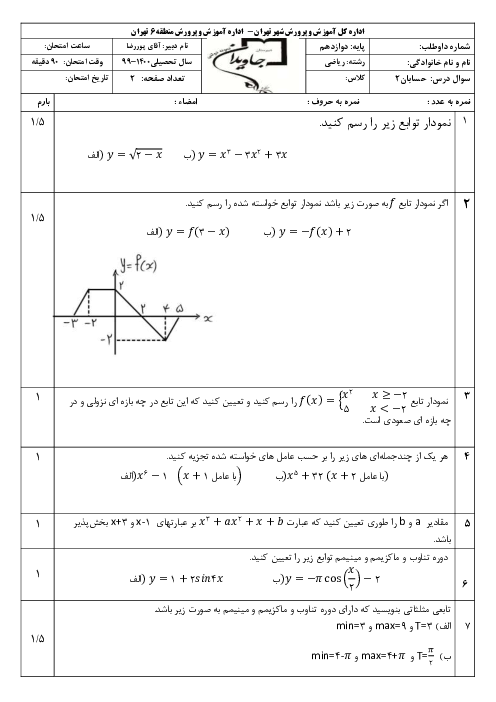
درس 2: تابع درجه سوم، توابع یکنوا و بخشپذیری و تقسیم
حسابان (2)
دوازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
تابع با ضابطهٔ $f(x)=\left| 2x-6 \right|-\left| x+1 \right|$، در یک بازه، صعودی است. ضابطهٔ معکوس آن در این بازه، کدام است؟
1 )
$-x+7;x\rangle 8$
2 )
$\frac{1}{3}x+2;x\rangle 3$
$x+7;x\rangle -4$
4 )
$\frac{1}{2}x-1;-4\langle x\langle 8$