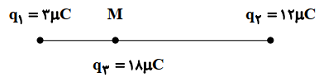برآیند نیروهای وارد بر بار، ${{q}_{3}}$ روی خط واصل دو بار هم نام، در فاصلهٔ میان آن دو و نزدیک به بار با اندازهٔ کوچک‌تر صفر می‌شود.

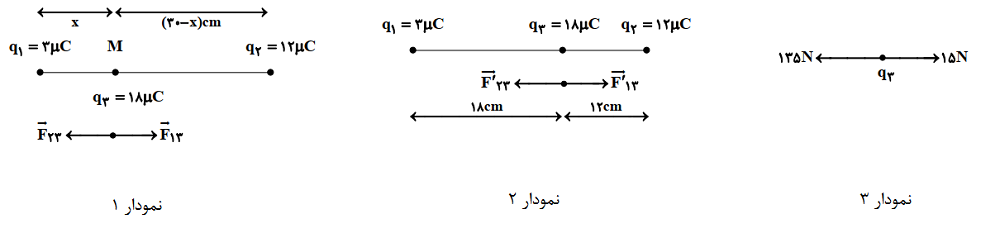
به نمودار 1 توجه شود.

در نقطهٔ M نیروی وارد بر بار${{q}_{3}}$ از سوی دو بار دیگر، هم‌اندازه و در خلاف جهت هم هستند:

${{F}_{13}}={{F}_{23}}\Rightarrow k\frac{\left| {{q}_{1}} \right|\left| {{q}_{3}} \right|}{{{x}^{2}}}=k\frac{\left| {{q}_{2}} \right|\left| {{q}_{3}} \right|}{{{(r-x)}^{2}}}\Rightarrow \frac{3}{{{x}^{2}}}=\frac{12}{{{(30-x)}^{2}}}\Rightarrow x=10cm$

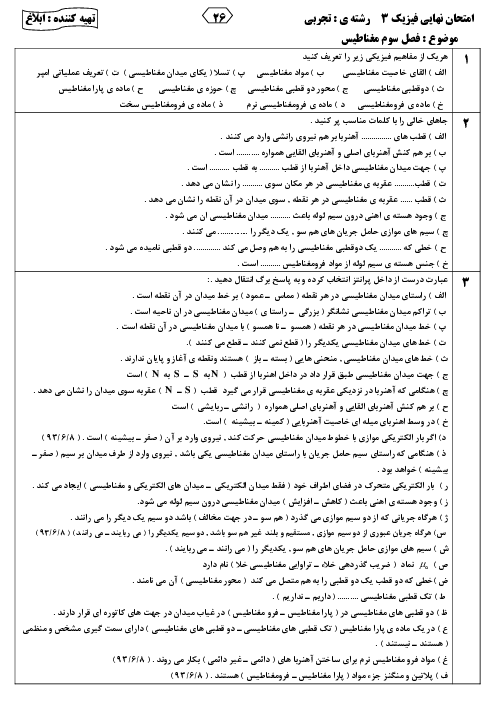
اگر ${{q}_{3}}$ را 8 سانتیمتر به بار بزرگ‌تر نزدیک کنیم، داریم:

به نمودار 2 توجه شود.

$\begin{align}  & {{{{F}'}}_{13}}=k\frac{\left| {{q}_{1}} \right|\left| {{q}_{3}} \right|}{r_{13}^{2}}=\frac{9\times {{10}^{9}}\times 3\times {{10}^{-6}}\times 18\times {{10}^{-6}}}{324\times {{10}^{-4}}}=15N \\  & {{{{F}'}}_{23}}=k\frac{\left| {{q}_{2}} \right|\left| {{q}_{3}} \right|}{r_{23}^{2}}=\frac{9\times {{10}^{9}}\times 12\times {{10}^{-6}}\times 18\times {{10}^{-6}}}{144\times {{10}^{-4}}}=135N \\  & {{{{F}'}}_{T,3}}={{{{F}'}}_{23}}-{{{{F}'}}_{13}}=135-15=120N \\ \end{align}$

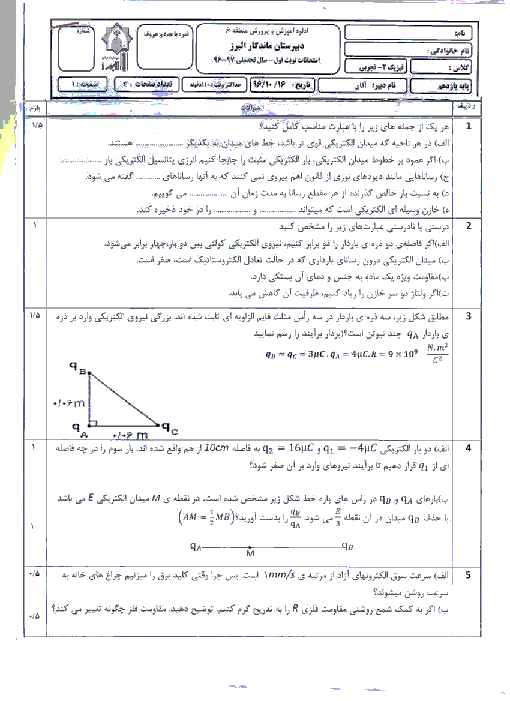
به نمودار 3 توجه شود.

نیروی وارد از سوی دو بار ${{q}_{1}}$ و ${{q}_{2}}$ بر بار ${{q}_{3}}$ در خلاف جهت هم است، درنتیجه اندازهٔ برآیند این دونیرو 120 نیوتون می‌شود.