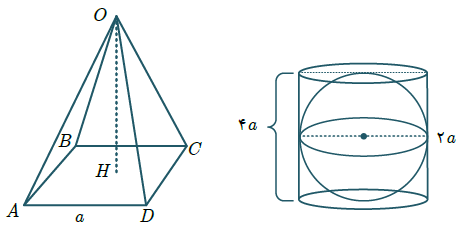
شعاع قاعده استوانه $ = 2a$
ارتفاع استوانه $ = 4a$
$OH = 6$
$\begin{gathered}
{V_1} = {V_2} \Rightarrow \frac{1}{3}S \times h = S \times h \hfill \\
\frac{1}{3}({a^2}) \times 6 = {(2a)^2} \times \pi \times 4a \Rightarrow \hfill \\
\end{gathered} $
$2{a^2} = 16{a^3}\pi \to 16{a^3}\pi - 2{a^2} = 0 \to 2{a^2}(8a\pi - 1) = 0 \to a = 0\,\,,\,\,a = \frac{1}{{8\pi }}$
شعاع کره $ = 2 \times (\frac{1}{{88}}) = \frac{1}{{4\pi }}$
کره $V = \frac{4}{3}\pi $
$ = \frac{4}{3}\pi {(\frac{1}{{4\pi }})^3} = \frac{{\cancel{4}}}{3} \times \cancel{\pi } \times \frac{1}{{\mathop {\cancel{{64}}}\limits_{16} \mathop {\cancel{{{\pi ^3}}}}\limits_{{\pi ^2}} }} = \frac{1}{{48{\pi ^2}}}$