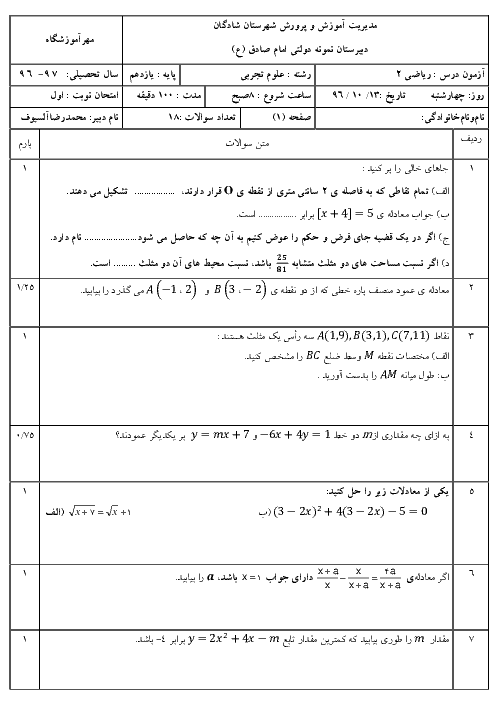
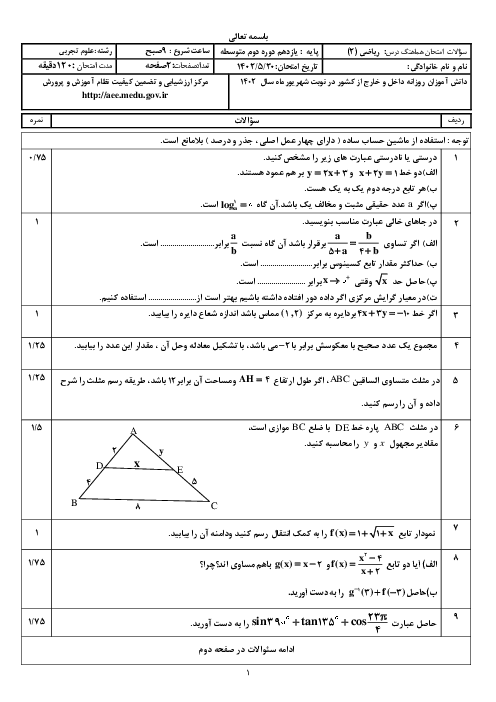
درس 1: آشنایی با برخی از انواع توابع
ریاضی (2)
یازدهم
دوره دوم متوسطه- نظری
علوم تجربی
درسنامه آموزشی این مبحث
دو تابع $f(x)=\left\{ \begin{matrix} 1,x\gt a \\ b,x\lt c \\ \end{matrix} \right.$ و $g(x)=\frac{\left| x-2 \right|}{x-2}$ برابرند. مقدار $a+b+c$ کدام است؟
تحلیل ویدئویی تست
محسن ذوالفقاری 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...