اگر دامنه تابع به‌صورت باشد، در این صورت کدام است؟

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

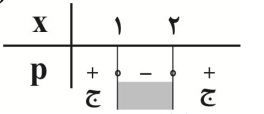
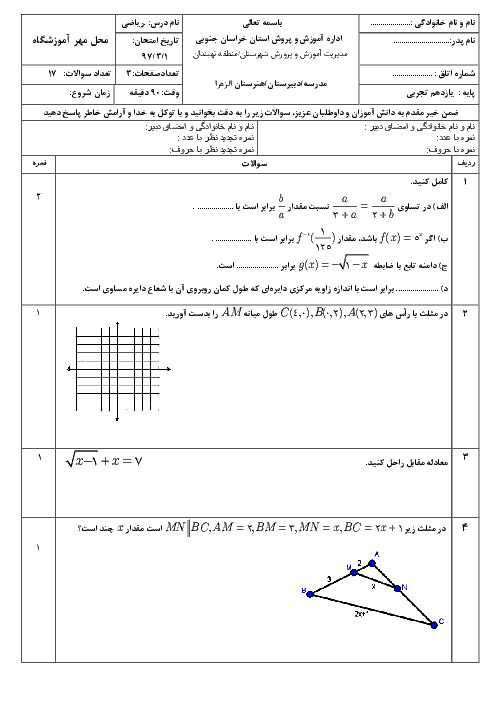
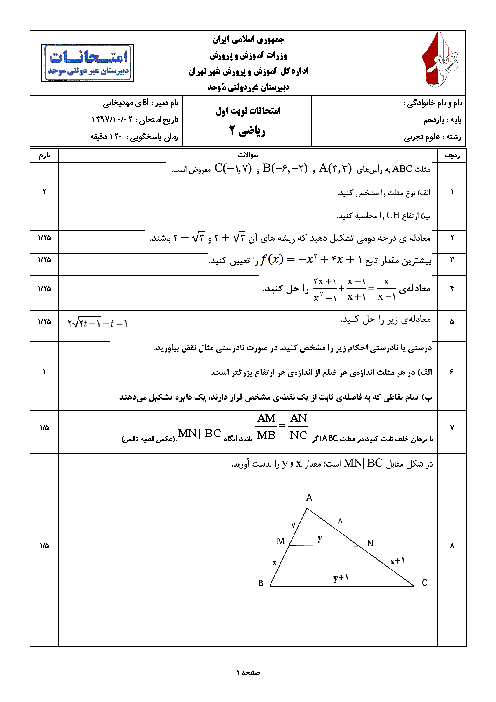
درس 1: آشنایی با برخی از انواع توابع ریاضی (2) یازدهم دوره دوم متوسطه- نظری علوم تجربی درسنامه آموزشی این مبحث

اگر دامنه تابع $f(x)=\frac{{{x}^{2}}+1}{\sqrt{2{{x}^{2}}-6x+a}}$ به‌صورت $x\in (-\infty ,1)\bigcup (b,+\infty )$ باشد، در این صورت $a\times b$ کدام است؟ $(b\ge 1)$

1 )

2 )

3 )

4 )

نمایش پاسخ

با توجه به حدود دامنه x (1 ریشهٔ مخرج کسر است:

$\sqrt{2{{x}^{2}}-6x+a=0}\xrightarrow{x=1}\sqrt{2-6+a}=0\Rightarrow \sqrt{-4+a}=0\xrightarrow{{}}-4+a=0\Rightarrow a=4\Rightarrow f(x)=\frac{{{x}^{2}}+1}{\sqrt{2{{x}^{2}}-6x+4}}$

برای محاسبه دامنهٔ تابع (f(x باید عبارت زیر رادیکال را که در مخرج است، بزرگ‌تر از صفر قرار دهیم، پس:

$2{{x}^{2}}-6x+4\gt 0\xrightarrow{\div 2}{{x}^{2}}-3x+2\gt 0\Rightarrow (x-1)(x-2)\gt 0$

با توجه به جدول تعیین علامت

$x\lt 1$ یا $x\gt 2\to x\in (-\infty ,1)\bigcup (2,+\infty )\Rightarrow b=2\Rightarrow a\times b=4\times 2=8$