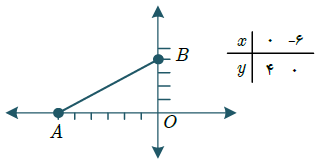
خط $y = \frac{2}{3}x + 4$ محورهای مختصات را در نقاط A و B قطع می‌کند. محیط و مساحت مثلث OAB کدام است؟
محیط $10 + 2\sqrt {13} = $ و مساحت $12 = $
2 )
محیط $12 = $ و مساحت $12 = $
3 )
محیط $6 + 2\sqrt {13} = $ و مساحت $6 = $
4 )
محیط $10 + 2\sqrt {13} = $ و مساحت $6 = $
پاسخ تشریحی :
تحلیل ویدئویی تست
عادل علی پناه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...