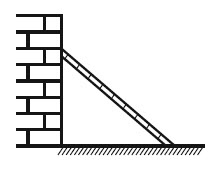
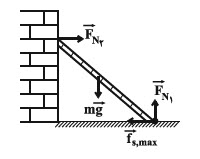
چون نردبان در آستانۀ سُر خوردن (حركت) است، بنابراين نيروی خالص وارد بر نردبان در دو راستای افقی و عمودی صفر است، بنابراين داريم:

${{F}_{net}}=0\Rightarrow \left\{ \begin{matrix}    {{\left( {{F}_{net}} \right)}_{y}}=0\Rightarrow {{F}_{{{N}_{1}}}}=mg=200N  \\    {{\left( {{F}_{net}} \right)}_{x}}=0\Rightarrow {{F}_{{{N}_{2}}}}={{f}_{s,\max }}\begin{matrix}    {} & \left( * \right)  \\ \end{matrix}  \\ \end{matrix} \right.$

اندازۀ نيروی اصطكاك ايستايی برابر است با:

${{f}_{s,\max }}={{\mu }_{s}}{{F}_{{{N}_{1}}}}=0/75\times 200=150N\xrightarrow{\left( * \right)}{{F}_{{{N}_{2}}}}={{f}_{s,\max }}=150N$

از طرف سطح افقی دو نیروی عمود بر هم \[{{\overrightarrow{f}}_{s,\max }},{{\overrightarrow{F}}_{{{N}_{1}}}}\] بر نردبان وارد می‌شود، بنابراین:

$R=\sqrt{F_{{{N}_{1}}}^{2}+f_{s,\max }^{2}}=\sqrt{{{200}^{2}}+{{150}^{2}}}=250N$

در نهایت می‌توان نوشت:

$\frac{{{F}_{{{N}_{2}}}}}{R}=\frac{150}{250}=\frac{3}{5}$