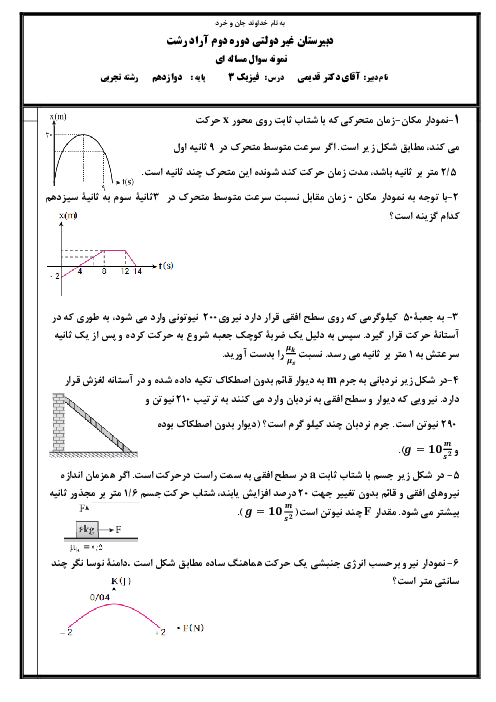
ابتدا سرعت‌های دو خودرو را بر حسب $\frac{m}{s}$ به‌دست می‌آوريم، داريم: 

${{v}_{{}^\circ }}A=90\frac{km}{h}=\frac{90}{3/6}\frac{m}{s}=25\frac{m}{s}$

${{v}_{B}}=18\frac{km}{h}=\frac{18}{3/6}=5\frac{m}{s}$

در لحظه‌ای كه ماشين $A$ شروع به ترمز گرفتن می‌كند ماشين $B$ را در مکان ${{x}_{{}^\circ }}B=0$ و ماشين $A$ را در مکان ${{x}_{{}^\circ }}A$ فرض می‌کنیم.

${{x}_{A}}=\frac{1}{2}{{a}_{A}}{{t}^{2}}+{{v}_{{}^\circ }}t+{{x}_{{}^\circ A}}$

$\xrightarrow[{{a}_{A}}=-4\frac{m}{{{s}^{2}}}]{{{v}_{{}^\circ A}}=25\frac{m}{s}}$

${{x}_{B}}={{v}_{B}}t+{{x}_{{}^\circ B}}\xrightarrow[{{v}_{B}}=5{m}/{s}\;]{{{x}_{{}^\circ B}}=0}{{x}_{B}}=5t$

در لحظه‌ای كه دو متحرک در آستانهٔ برخورد به هم هستند، ${{x}_{A}}={{x}_{B}}$ است.

${{x}_{A}}={{x}_{B}}\Rightarrow -2{{t}^{2}}+25t+{{x}_{{}^\circ A}}=5t\Rightarrow -2{{t}^{2}}+20t+{{x}_{{}^\circ A}}=0$

برای اين‌كه دو اتومبيل به يكديگر برخورد نكنند، می‌بايست اين معادله جواب نداشته باشد يا حداكثر يک جواب داشته باشد.

$\Delta \le 0\Rightarrow 400+8{{x}_{{}^\circ A}}\le 0\Rightarrow {{x}_{{}^\circ A}}\le -50m$

بنابراين در لحظه‌ای كه فاصلهٔ دو اتومبيل از يكديگر 50 متر می‌شود، راننده بايد ترمز بگيرد. چون قبل از گرفتن ترمز، هر دو اتومبيل با سرعت ثابت در حال حركت هستند. لحظه‌ای كه فاصلهٔ دو اتومبيل $50m$ می‌شود را به دست می‌آوريم:

${{x}_{A}}={{v}_{A}}t+{{x}_{{}^\circ A}}\xrightarrow[{{v}_{A}}=25\frac{m}{s},{{v}_{B}} =5\frac{m}{s}]{{{x}_{{}^\circ A}}=-120m,{{x}_{{}^\circ B}}=0}\left\{ \begin{matrix} {{x}_{A}}=25t-120  \\ {{x}_{B}}=5t  \\ \end{matrix} \right.$

$\xrightarrow[{}]{{{x}_{A}}-{{x}_{B}}=-50m}-50=20t-120\Rightarrow t=\frac{70}{20}=3/5s$