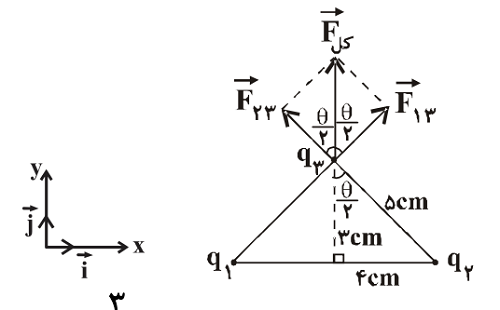
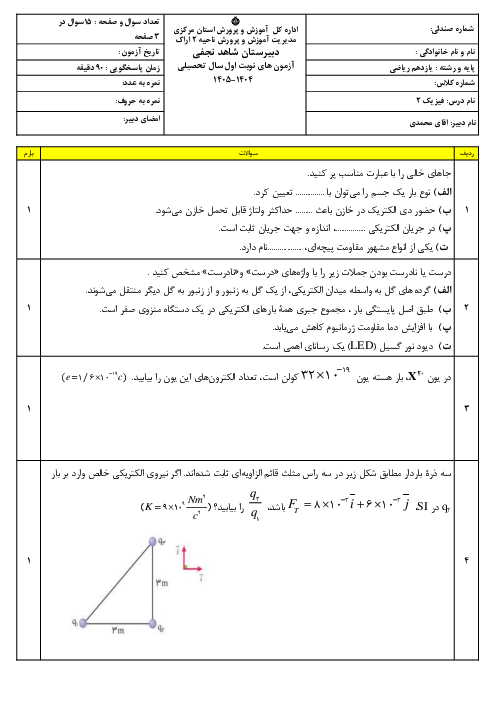
مطابق شکل زیر، برایند نیروهای الکتریکی وارد بر بار ${{q}_{3}}$ برابر کل $\overrightarrow{F}$ است، داریم:

$\begin{align}
  & {{F}_{13}}=k\frac{\left| {{q}_{1}} \right|\left| {{q}_{3}} \right|}{{{r}^{2}}}=9\times {{10}^{9}}\times \frac{5\times {{10}^{-6}}\times 3\times {{10}^{-6}}}{25\times {{10}^{-4}}}=54N \\
 & {{F}_{23}}=k\frac{\left| {{q}_{2}} \right|\left| {{q}_{3}} \right|}{{{r}^{2}}}=9\times {{10}^{9}}\times \frac{5\times {{10}^{-6}}\times 3\times {{10}^{-6}}}{25\times {{10}^{-4}}}=54N \\
 & {{\overrightarrow{F}}_{13}}={{F}_{13,x}}\overrightarrow{i}+{{F}_{13,y}}\overrightarrow{j}=(54\sin \frac{\theta }{2})\overrightarrow{i}+(54\cos \frac{\theta }{2})\overrightarrow{j} \\
 & {{\overrightarrow{F}}_{23}}={{F}_{23,x}}\overrightarrow{i}+{{F}_{23,y}}\overrightarrow{j}=(-54\sin \frac{\theta }{2})\overrightarrow{i}+(54\cos \frac{\theta }{2})\overrightarrow{j} \\
 & \Rightarrow {{\overrightarrow{F}}_{Total}}=2\times (54\cos \frac{\theta }{2})\overrightarrow{j} \\
\end{align}$

با توجه به تصویر

${{F}_{Total}}=2F\cos \frac{\theta }{2}=2\times 54\times \frac{3}{5}=64/8N$