قسمت 3: حرکت با شتاب ثابت
فیزیک (3) ریاضی
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
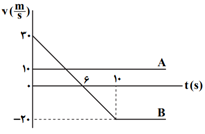
نمودار سرعت - زمان دو متحرک $A$ و $B$ كه روی يک خط راست حركت میكنند، مطابق شكل است. اگر مكان آنها در لحظۀ $t=0$ بهترتيب ${{x}_{{}^\circ A}}=-50m$ و ${{x}_{{}^\circ B}}=+150m$ باشد، در چه زمانی دو متحرک به هم میرسند؟