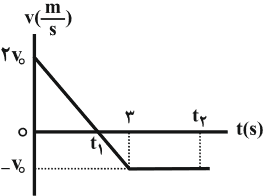
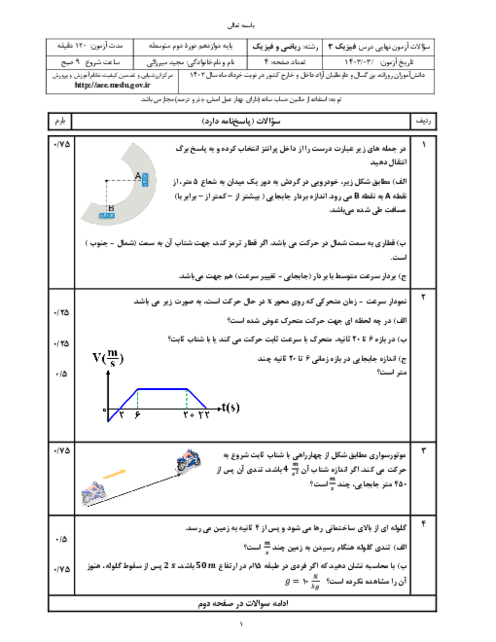
متحرک در لحظهٔ $t=0$ از مبدأ مکان عبور کرده است، بنابراین در لحظه‌ای که دوباره از مبدأ مکان عبور می‌کند، جابه‌جایی آن برابر  با صفر می‌شود. از طرفی می‌دانیم مساحت زیر نمودار سرعت - زمان برابر با جابه‌جایی متحرک است. بنابراین ابتدا با استفاده از تشابه مثلث‌ها، لحظه‌ای که سرعت صفر می‌شود را در می‌یابیم. داریم:

$\frac{2{{v}_{0}}}{{{v}_{0}}}=\frac{{{t}_{1}}}{3-{{t}_{1}}}\Rightarrow {{t}_{1}}=2s$

از لحظهٔ صفر تا $t=2s$، نمودار سرعت - زمان بالای محور زمان است و بنابراین جابه‌جایی آن مثبت است. داریم:

${{S}_{1}}=\frac{2\times 2{{v}_{0}}}{2}=2{{v}_{0}}$

(شکل)
از لحظهٔ ${{t}_{1}}=2s$ به بعد، نمودار سرعت - زمان زیر محور زمان است و بنابراین جابه‌جایی آن منفی است. متحرک در لحظهٔ ${{t}_{2}}$ به مبدأ مکان باز می‌گردد، داریم:

$\left| {{S}_{2}} \right|=\frac{({{t}_{2}}-{{t}_{1}})+({{t}_{2}}-3)}{2}\times {{v}_{0}}$ 

$\xrightarrow{{{t}_{1}}=2s}\left| {{S}_{2}} \right|=\frac{({{t}_{2}}-2)+({{t}_{2}}-3)}{2}\times {{v}_{0}}=\frac{2{{t}_{2}}-5}{2}{{v}_{0}}$

در نتیجه داریم:

 ${{S}_{1}}=\left| {{S}_{2}} \right|\Rightarrow 2{{v}_{0}}=\frac{2{{t}_{2}}-5}{2}{{v}_{0}}\Rightarrow {{t}_{2}}=4/5s$