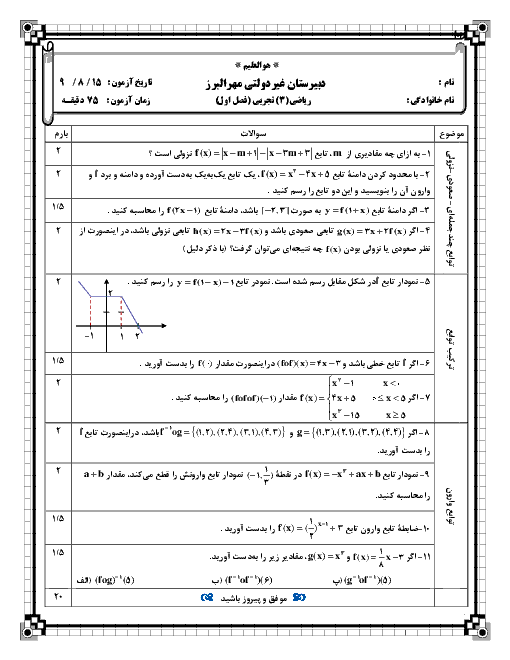
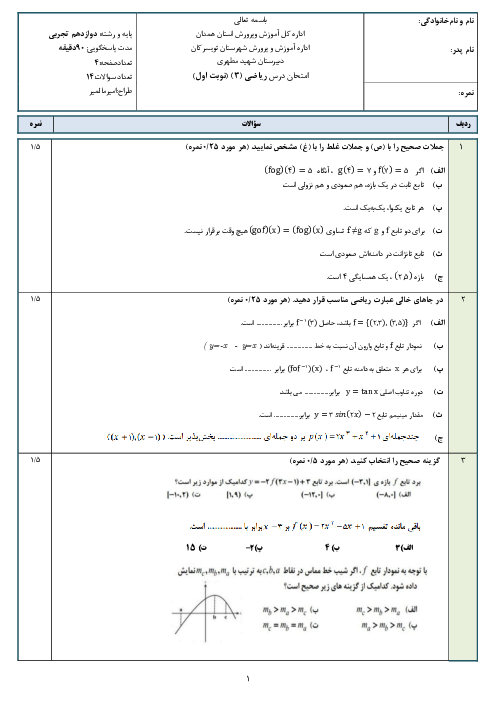
نکتۀ 1: ${a^3} - {b^3} = (a - b)({a^2} + ab + {b^2})$

نکتۀ 2: گاهی صورت یا مخرج تابع $\frac{f}{g}$ شامل یک عبارت رادیکالی است و 

$\mathop {\lim }\limits_{x \to a} f(x) = \mathop {\lim }\limits_{x \to a} g(x) = 0$. در این حالت برای محاسبۀ حد $\frac{f}{g}$ در نقطۀ a لازم است ابتدا صورت و مخرج را در یک عبارت رادیکالی ضرب کنیم تا عامل 

(x - a) یا عبارتی که موجب صفر شدن f و g شده است، در صورت و مخرج ظاهر شود تا با ساده کردن آن از صورت و مخرج بتوانیم مقدار حد را در صورت وجود به دست آوریم.

نکتۀ 3: قضیه: فرض کنیم $\mathop {\lim }\limits_{x \to a} f(x) = L \ne 0$ و

$\mathop {\lim }\limits_{x \to a} g(x) = 0$ ، در این صورت:

اگر $L \lt 0$ و تابع g(x) در همسایگی محذوفی از a مثبت باشد، آن‌گاه: 

$\mathop {\lim }\limits_{x \to a} \frac{{f(x)}}{{g(x)}} =  - \infty $

ابتدا باید با ضرب کردن صورت و مخرج کسر در یک عبارت جبری، ریشۀ سوم را در صورت از بین می‌بریم، سپس به حذف عامل صفر کننده می‌پردازیم:

$\mathop {\lim }\limits_{x \to {0^ + }} \frac{{\root 3 \of {8 - \sqrt x }  - 2}}{x} \times \frac{{(\root 3 \of {8 - \sqrt x {)^2}}  + 2\root 3 \of {8 - \sqrt x }  + {2^2})}}{{(\root 3 \of {8 - \sqrt x {)^2}}  + 2\root 3 \of {8 - \sqrt x }  + {2^2})}} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{8 - \sqrt x  - 8}}{{x \times (4 + 4 + 4)}} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{ - \sqrt x }}{{12x}} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{ - 1}}{{12\sqrt x }} = \frac{{ - 1}}{{{0^ + }}} =  - \infty $

توجه کنید در کسر $\frac{{ - 1}}{{12\sqrt x }}$ حد صورت برابر 1- است و مخرج با مقادیر مثبت به صفر میل می‌کند، پس حاصل حد، منفی بی‌نهایت است.