درس 1: تبدیل نمودار توابع
حسابان (2)
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
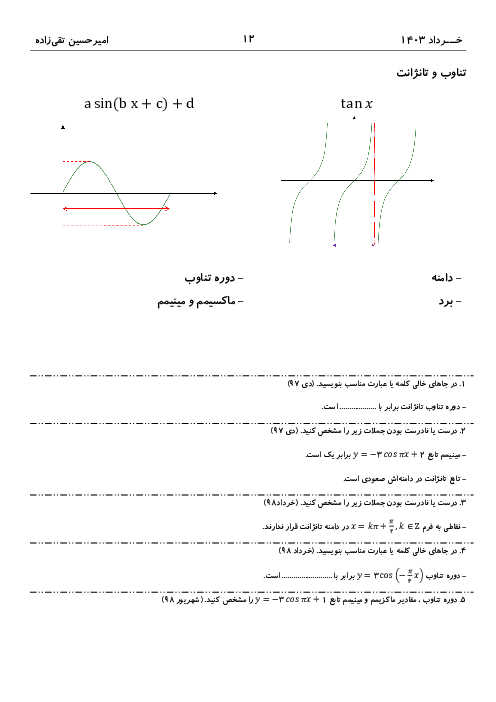
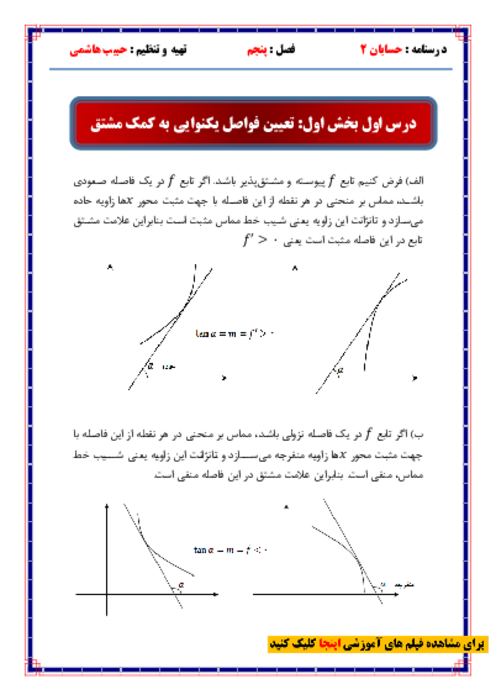
نمودار تابع $y=f(x)$ مفروض است. اگر ابتدا نمودار را نسبت به محور $y$ها قرينه كنيم، سپس آن را 2 واحد در راستای محور $x$ها به‌طرف راست منتقل كنيم و در انتها با ضريب 2 آن را در راستای عمودی انبساط دهيم، كدام تابع به‌دست می‌آيد؟
1 )
$g(x)=2f(-x-2)$
$g(x)=2f(-x+2)$
3 )
$g(x)=\frac{1}{2}f(-x-2)$
4 )
$g(x)=\frac{1}{2}f(-x+2)$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...