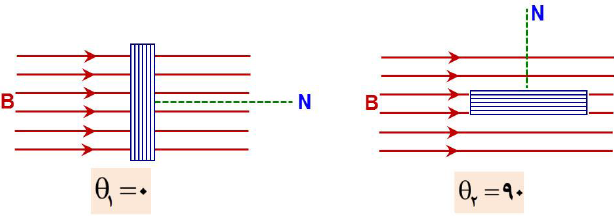
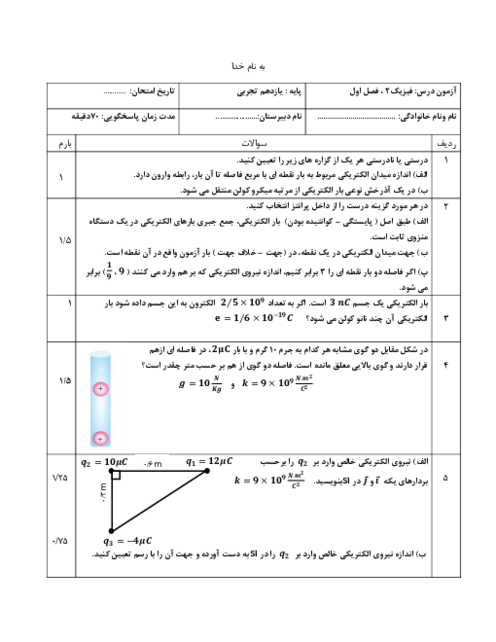
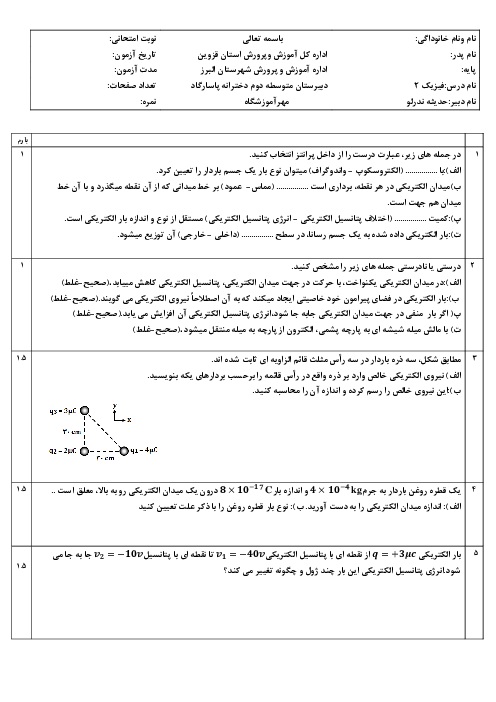
در این مسئله تغییرات شار مغناطیسی ناشی از تغییر زاویه بین خط‌های میدان مغناطیسی (B) و نیم خط عمود بر سطح قاب (N) است.

$\left. \begin{matrix}{{\Phi }_{1}}=BA\cos {{\theta }_{1}}  \\{{\Phi }_{2}}=BA\cos {{\theta }_{2}}  \\\end{matrix} \right\}\to \Delta \Phi =BA\left[ \cos {{\theta }_{2}}-\cos {{\theta }_{1}} \right]$
$\Delta \Phi =\left( 0/5\times {{10}^{-4}} \right)\times (30\times {{10}^{-4}})\times \left[ \cos 90-\cos 0 \right]$
$\Delta \Phi =-15\times {{10}^{-8}}wb$

این تغییرات شار باعث ایجاد نیروی محرکه‌ی القایی در مدار می‌شود که به صورت زیر به دست می‌آید.

$\left| \overline{\varepsilon } \right|=\left| -N\frac{\Delta \Phi }{\Delta t} \right|\to \left| \overline{\varepsilon } \right|=\left| -N\frac{\Delta \Phi }{\Delta t} \right|\to \left| \overline{\varepsilon } \right|=\left| -1000\times \frac{-15\times {{10}^{-8}}}{2\times {{10}^{-2}}} \right|\to \left| \overline{\varepsilon } \right|=7/5\times {{10}^{-3}}v$