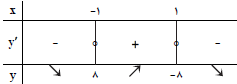
نقطه‌ای به طول $-1$ برای تابع $f(x)=\frac{a}{x}-2{{x}^{3}}$ نقطه‌ای بحرانی است. كدام گزينه درمورد اكسترمم تابع $f$ درست است؟
1 )
نقطهٔ $(-1,8)$ ماكزيمم نسبی است.
نقطهٔ $(1,-8)$ ماكزيمم نسبی است.
3 )
نقطهٔ $(-1,-4)$ مینیمم نسبی است.
4 )
نقطهٔ $(-1,4)$ مینیمم نسبی است.
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...