نکته: در بیضی بین $a$، $b$ و $c$ هموارهٔ رابطهٔ ${{a}^{2}}={{b}^{2}}+{{c}^{2}}$ برقرار است.

نکته: در بیضی طول قطر بزرگ برابر $2a$ است.

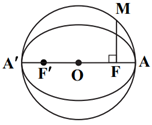
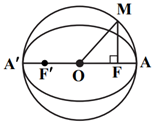
با توجه به شکل مقابل، چون شعاع دایره برابر $OA=a$ است، داریم:

$OM=OA=a$

$OF=c\Rightarrow O{{M}^{2}}=O{{F}^{2}}+M{{F}^{2}}\Rightarrow {{a}^{2}}={{c}^{2}}+M{{F}^{2}}\Rightarrow {{b}^{2}}+{{c}^{2}}={{c}^{2}}+M{{F}^{2}}\Rightarrow MF=b\Rightarrow b=2(*)$

خروج از مرکز بیضی برابر $\frac{2}{3}$ است:

$e=\frac{c}{a}=\frac{2}{3}\Rightarrow c=\frac{2}{3}a\Rightarrow {{c}^{2}}=\frac{4}{9}{{a}^{2}}\Rightarrow {{a}^{2}}-{{b}^{2}}=\frac{4}{9}{{a}^{2}}$

$\Rightarrow {{a}^{2}}-\frac{4}{9}{{a}^{2}}={{b}^{2}}\Rightarrow \frac{5}{9}{{a}^{2}}={{b}^{2}}\Rightarrow \frac{a\sqrt{5}}{3}=b\xrightarrow{(*)}\frac{a\sqrt{5}}{3}=2\Rightarrow a=\frac{6}{\sqrt{5}}=\frac{6\sqrt{5}}{5}$

بنابراین:

قطربزرگ $=2a=2\times \frac{6\sqrt{5}}{5}=\frac{12\sqrt{5}}{5}$