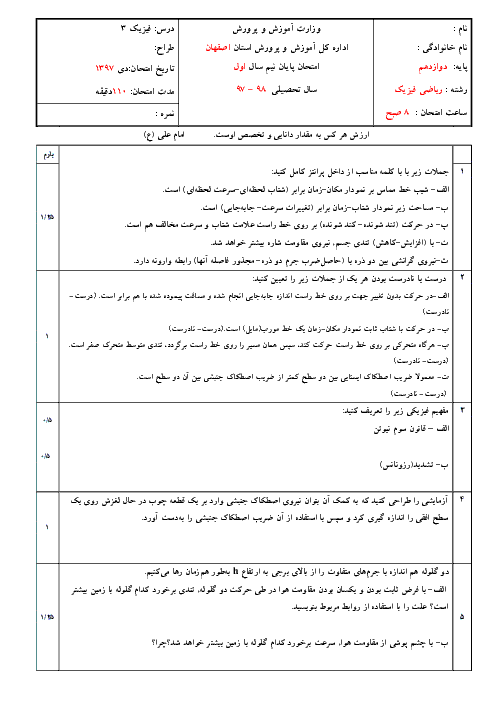
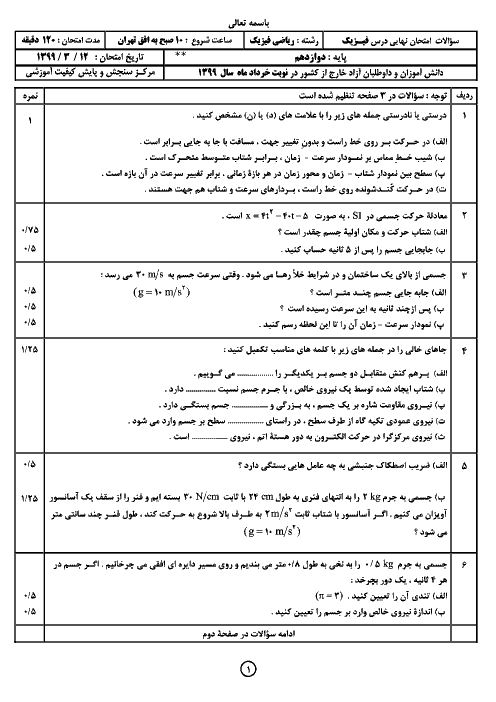
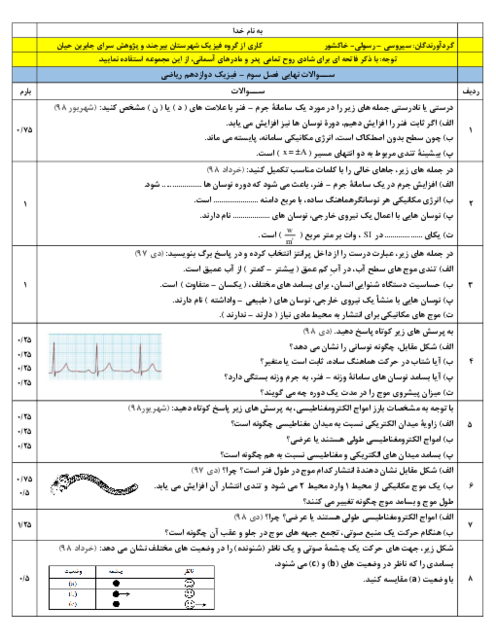
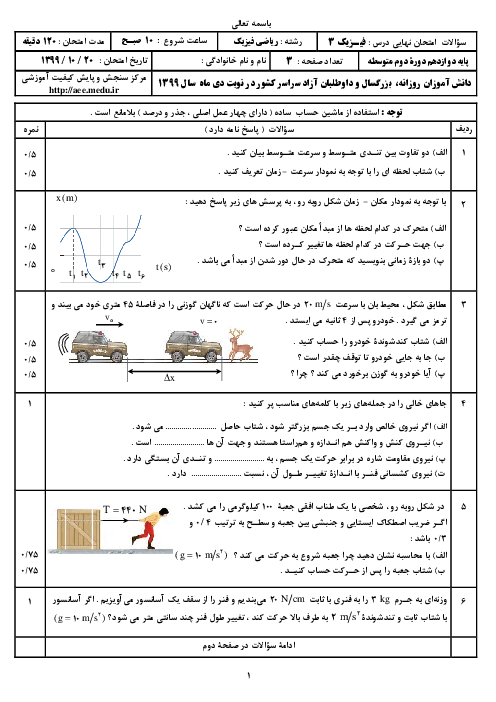
گام اول: از آن‌جایی که هر دو جسم در ابتدا ساکن بوده و بر هر دو، نیروی خالص ثابت اثر می‌کند، نتیجه می‌گیریم نوع حرکت جسم راست‌خط شتاب ثابت است.

با توجه به قانون دوم نیوتون، شتاب‌ها را بر حسب ${{m}_{1}}$ و ${{m}_{2}}$ می‌نویسیم: ${{a}_{1}}=\frac{F}{{{m}_{1}}}$ و ${{a}_{2}}=\frac{F}{{{m}_{2}}}$ 

گام دوم: اندازه‌ی سرعت‌های $\overrightarrow{{{V}_{1}}}$ و $\overrightarrow{{{V}_{2}}}$ را هم حساب می‌کنیم: 

${{V}_{1}}=\sqrt{{{9}^{2}}+{{(-12)}^{2}}}=15m/s,{{V}_{2}}=\sqrt{{{3}^{2}}+{{(-4)}^{2}}}=5m/s$ 

حالا می‌توانیم به کمک رابطه‌ی $V=at+{{V}_{{}^\circ }}$ نسبت جرم‌ها را حساب کنیم:

$\left\{ _{{{V}_{2}}={{a}_{2}}t+0\Rightarrow 5=\frac{F}{{{m}_{2}}}t}^{{{V}_{1}}={{a}_{1}}t+0\Rightarrow 15=\frac{F}{{{m}_{1}}}t} \right.$ 

دو طرف رابطه‌های بالا را به هم تقسیم می‌کنیم: $\frac{15}{5}=\frac{\frac{F}{{{m}_{1}}}t}{\frac{F}{{{m}_{2}}}}\Rightarrow \frac{{{m}_{2}}}{{{m}_{1}}}=3$ 

گام سوم: چون حرکت از حال سکون شروع شده و حرکت راست‌خط شتاب ثابت است، مسافت طی شده برابر جابه‌جایی است و داریم:

$\left\{ _{{{l}_{2}}=\Delta {{X}_{2}}=\frac{1}{2}{{a}_{2}}{{t}^{2}}=\frac{1}{2}\times \frac{F}{{{m}_{2}}}{{t}^{2}}}^{{{l}_{1}}=\Delta {{X}_{1}}=\frac{1}{2}{{a}_{1}}{{t}^{2}}=\frac{1}{2}\times \frac{F}{{{m}_{1}}}{{t}^{2}}}\Rightarrow \frac{{{l}_{1}}}{{{l}_{2}}} \right.=\frac{\frac{1}{2}\times \frac{F}{{{m}_{1}}}{{t}^{2}}}{\frac{1}{2}\times \frac{F}{{{m}_{2}}}{{t}^{2}}}=\frac{{{m}_{2}}}{{{m}_{1}}}=3$