اتومبیلی فاصله‌ی بین دو شهر را در جاده‌ای مستقیم و افقی با سرعت متوسط طی می‌کند، سپس مسیر قبلی را باز گشته و نیمی از فاصله‌ی بین دو شهر را با سرعت متوسط طی می‌کند.… | فیزیک (3) ریاضی دوازدهم شماره 66969

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

قسمت 2: حرکت با سرعت ثابت فیزیک (3) ریاضی دوازدهم دوره دوم متوسطه- نظری علوم ریاضی درسنامه آموزشی این مبحث

اتومبیلی فاصله‌ی بین دو شهر را در جاده‌ای مستقیم و افقی با سرعت متوسط $60\frac{km}{h}$ طی می‌کند، سپس مسیر قبلی را باز گشته و نیمی از فاصله‌ی بین دو شهر را با سرعت متوسط $20\frac{km}{h}$ طی می‌کند. سرعت متوسط اتومبیل در کل این جابه‌جایی چند $\frac{m}{s}$ است؟

1 )

2 )

3 )

4 )

$\frac{10}{3}$

نمایش پاسخ

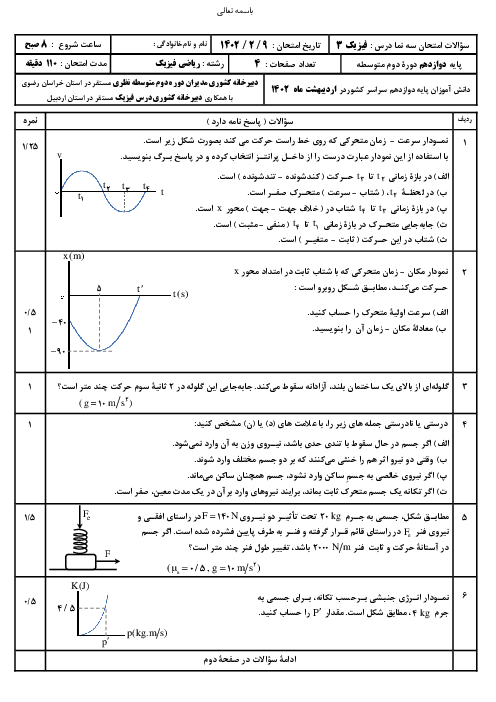
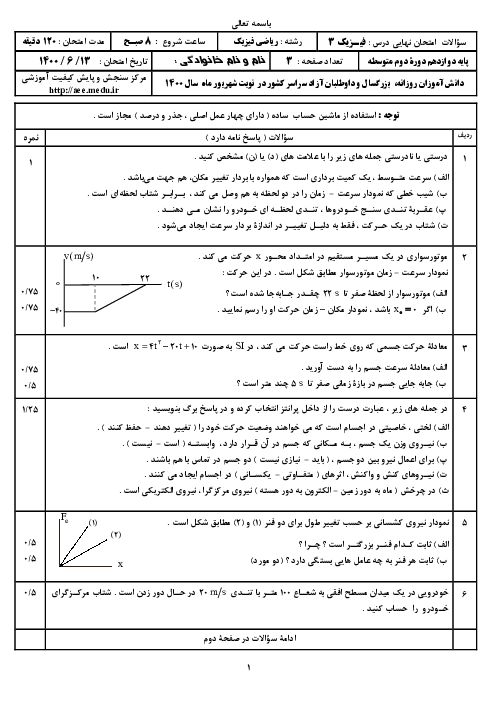
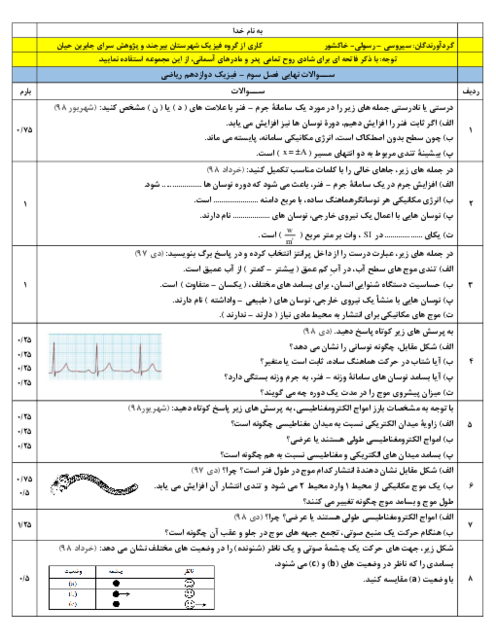
بنا به تعریف سرعت متوسط می‌توان نوشت:

$\left\{ \begin{matrix} \overline{v}=\frac{\Delta {{x}_{1}}+\Delta {{x}_{2}}+...}{{{t}_{1}}+{{t}_{2}}+...}\Rightarrow \overline{v}=\frac{\Delta {{x}_{1}}+\Delta {{x}_{2}}}{\frac{\Delta {{x}_{1}}}{{{\overline{v}}_{1}}}+\frac{\Delta {{x}_{2}}}{{{\overline{v}}_{2}}}} \\ \Delta x=\overline{v}\times t \\ \end{matrix} \right.$

باید توجه کرد چون در مرحله‌ی دوم، متحرک تغییر جهت داده است، جابه‌جایی این مرحله را با علامت مخالف جابه‌جایی در مرحله‌ی اول در نظر می‌گیریم:

$\overline{v}=\frac{x-\frac{x}{2}}{\frac{x}{{{v}_{1}}}+\frac{x}{2{{v}_{2}}}}\Rightarrow \overline{v}=\frac{{{v}_{1}}{{v}_{2}}}{2{{v}_{2}}+{{v}_{1}}}=\frac{60\times 20}{2\times 20+60}=12\frac{km}{h}\Rightarrow \overline{v}=\frac{12}{3/6}=\frac{10}{3}\frac{m}{s}$

گزارش اشکال