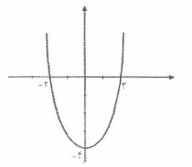
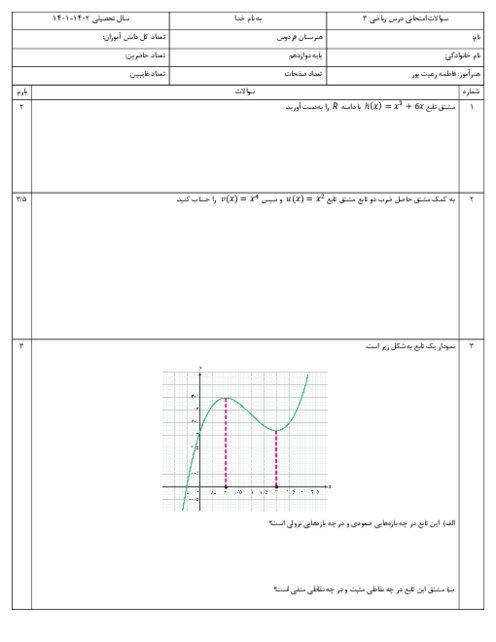
در مورد تابع $f\left( x \right)=\frac{1}{3}\left( {{x}^{3}}-12x+5 \right)$ کدام عبارت غلط است؟
1 )
مشتق تابع در بازه‌های $\left( -\infty ,-2 \right]$ و $\left[ 2,+\infty \right)$ مثبت است.
مشتق تابع در بازه‌های $\left( -\infty ,-2 \right]$ و $\left[ 2,+\infty \right)$ منفی است.
3 )
تابع f در بازه‌های $\left( -\infty ,-2 \right]$ و $\left[ 2,+\infty \right)$ صعودی است.
4 )
مشتق تابع f در بازه $\left( -2,2 \right)$ منفی است.
پاسخ تشریحی :
تحلیل ویدئویی تست
مهدی خلجی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...