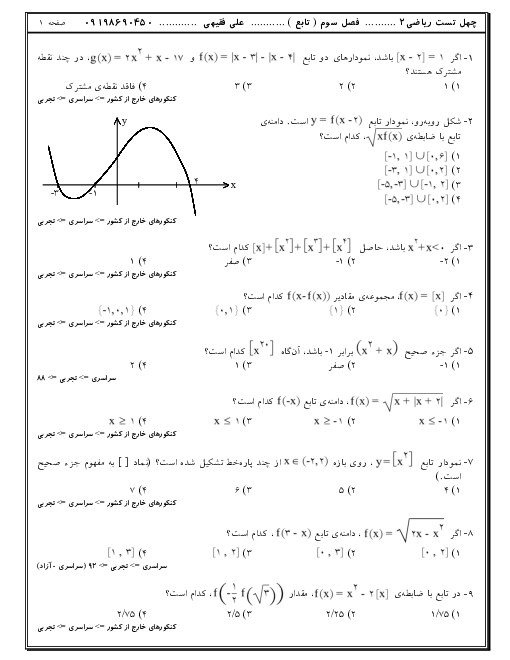
$(f + g)(x) = f(x) + g(x) = \left\{ \begin{gathered}
  2x + 1 + 3 - 2x\,\,\,\,\,\,\,\,\,\,\,x \geqslant 1 \hfill \cr 
  3x - 2 + 5x + 3\,\,\,\,\,\,\,\,\,\,x < 1 \hfill \cr 
 \end{gathered}  \right.$
$ \Rightarrow f(x) + g(x) = \left\{ \begin{gathered}
  4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x \geqslant 1 \hfill \cr 
  8x + 1\,\,\,\,\,\,\,\,x < 1 \hfill \cr 
 \end{gathered} \right.$

$(f - g)(x) = f(x) - g(x) = \left\{ \begin{gathered}
  2x + 1 - 3 + 2x\,\,\,\,\,\,\,\,\,\,\,x \geqslant 1 \hfill \cr 
  3x - 2 - 5x - 3\,\,\,\,\,\,\,\,\,\,x < 1 \hfill \cr 
 \end{gathered}  \right.$
$ \Rightarrow f(x) + g(x) = \left\{ \begin{gathered}
  4x - 2\,\,\,\,\,\,\,\,\,\,\,\,\,x \geqslant 1 \hfill \cr 
   - 2x - 5\,\,\,\,\,\,\,\,\,\,x < 1 \hfill \cr 
 \end{gathered}  \right.$