درس 2: رابطه‌های طولی در دایره
هندسه (2)
یازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
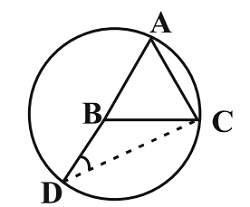
مثلث متساوی الاضلاع ABC را در نظر بگیرید. دایره‌ای به مرکز B، از دو رأس دیگر این مثلث نیز می‌گذرد. اگر امتداد AB، از سمت B دایره را در نقطهٔ D قطع کند، آن گاه $B\widehat{C}D$ کدام است؟
1 )
${{20}^{{}^\circ }}$
${{30}^{{}^\circ }}$
3 )
${{45}^{{}^\circ }}$
4 )
${{60}^{{}^\circ }}$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...