پودمان 1: کاربرد برخی تابع‌ها در زندگی روزمره
ریاضی3 فنی
دوازدهم
دوره دوم متوسطه- فنی
الکتروتکنیک (صنعت)
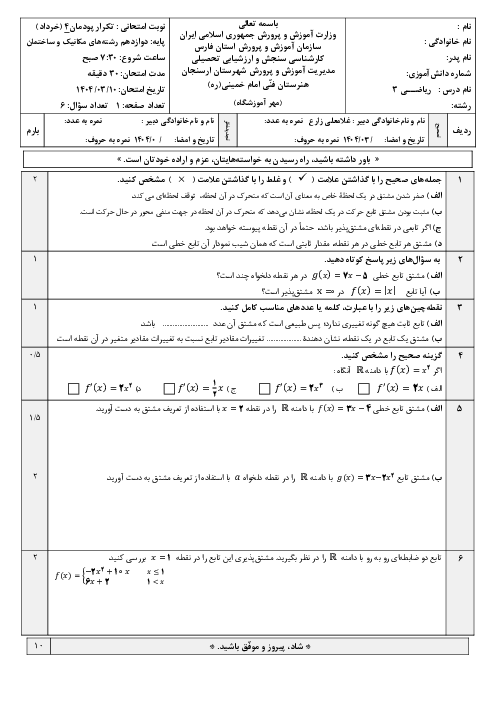
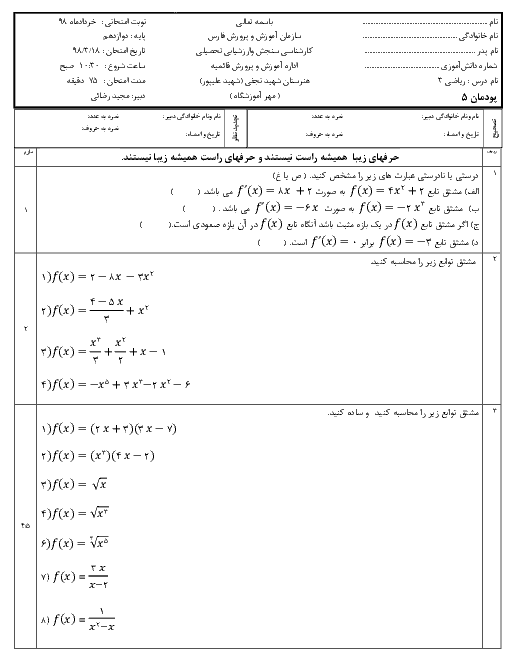
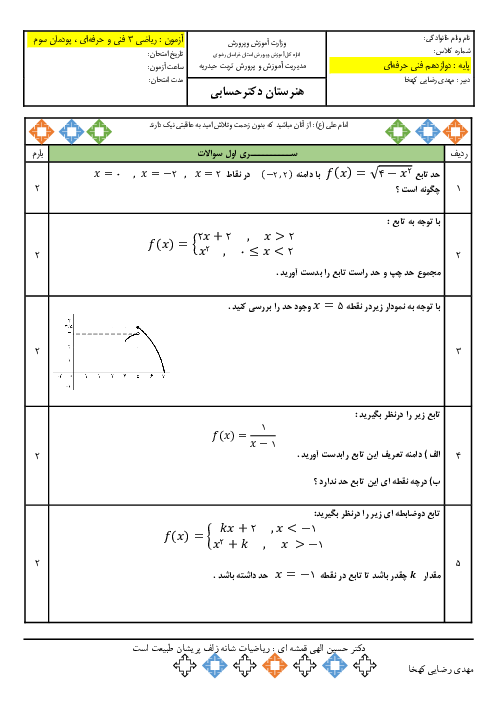
در تابع $f\left( x \right)=\left\{ \begin{matrix} x+1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\in z \\ 4{{x}^{2}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\notin z \\\end{matrix} \right.$ حاصل $f\left( \frac{1}{2} \right)+f\left( \sqrt{3} \right)+f\left( 8 \right)$ کدام است؟
تحلیل ویدئویی تست
راضیه هادیان 
زهرا شیخ الاسلامی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...