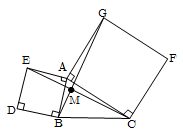
با توجه به فرضيات مسئله می‌دانيم نقاط $B$ و $E$ از نقطهٔ $A$ هم‌فاصله بوده $B\hat{A}E={{90}^{{}^\circ }}$ است. همچنین $AC=AG$ و $C\hat{A}G={{90}^{{}^\circ }}$ می‌باشد. لذا در دوران به اندازهٔ زاويهٔ 90 درجه در جهت عقربه‌های ساعت و به مركز نقطهٔ $A$، نقطهٔ $B$ به نقطهٔ $E$ و نقطهٔ $G$ به نقطهٔ $C$ انتقال می‌یابد.

در نتيجه پاره‌خط $CE$ دوران يافتهٔ $BG$ به اندازهٔ 90 درجه می‌باشد. از طرفی می‌دانيم دوران يک تبديل طولپا محسوب می‌شود، بنابراين: 

$BG=CE,B\hat{M}C={{90}^{{}^\circ }}$           (*)

همچنين از رابطهٔ (*) نتيجه می‌گيريم كه: 

$1)B\overset{\Delta }{\mathop{M}}\,C:M{{B}^{2}}+M{{C}^{2}}=B{{C}^{2}}$

$2)\left\{ \begin{matrix} B\hat{M}E+B\hat{D}E={{180}^{{}^\circ }}\Rightarrow MBDE  \\ C\hat{M}G+C\hat{F}G={{180}^{{}^\circ }}\Rightarrow MCFG  \\ \end{matrix} \right.$ محاطی است