در مورد اکسترهای نسبی تابع $f(x)=\left\{ \begin{matrix} \left[ x \right]\,\,\,\,\,\,\,\,\,x\notin Z \\ x-1\,\,\,\,\,\,x\in Z \\ \end{matrix} \right.$ کدام گزینه صحیح است؟ ($\left[ \, \right]$ نماد جزء صحیح است.)
1 )
نقاط با طول صحیح $max$ نسبی‌اند.
همه‌ی نقاط $R$ برای این تابع اکسترمم نسبی‌اند.
3 )
نقاط غیرصحیح فقط $min$ نسبی‌اند.
4 )
این تابع فاقد اکسترمم نسبی است.
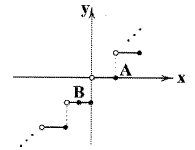
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...